|
Question 168781: Find the decimal equivalent of the new price for a 40/15/5 series trade discount.
Found 2 solutions by Mathtut, gonzo:
Answer by Mathtut(3670)   (Show Source):
You can put this solution on YOUR website!
let x be the original price
the new price would be (.6)(.85)(.95)=.4845 times x
so the new price would be 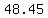 % of the original price
Answer by gonzo(654) (Show Source):
You can put this solution on YOUR website! as best i can determine, a 40/15/5 series trade discount would be calculated as follows:
let x = retail price.
x - .40*x = y = first discounted price.
y - .15*y = z = second discounted price.
z - .05*z = t = total discounted price.
-----
x - .4*x = (1-.4)*x = .6*x = y
y - .15*y = (1-.15)*y = .85*y = z
z - .05*z = (1-.05)*z = .95*z = t
----
since z = .85*y, then .95*z = .95*.85*y
since y = .6*x, then .95*z = .95*.85*.6*x
-----
based on the above, then t = total discount = .95*.85*.6*x = .4845*x
40/15/5 series discount is equivalent to a total discount of 48.45%
-----
first discount is taken off the retail price.
second discount is taken off the first discount price.
third discount is taken off the second discount price.
-----
example:
retail price = $20,192.00
first discount price = .6 * $20,192.00 = $12,115.20
second discount price = .85 * $12115.20 = $10,297.92
third discount price = .95 * $10,297.92 = $9,783.02
-----
overall discount price = .4845 * $20,192.00 = $9,783.02
-----
|
|
|
| |
