Solve the system by using an augmented matrix.
We need to end up with a matrix that looks like this:
Plan: by using row operations,
1. get a 0 on the left of the 2nd row.
2. get a 0 in the middle in the 1st row.
3. get a 1 on the left of the 1st row.
4. get a 1 in the middle of the 2nd row.
Also, any time a row can be easily divided through
by a constant, we will stop and do that too:
To get a 0 where the 3 is, we mentally multiply
each member of the first row by -3 and mentally
add it to 5 time the corresponding number and
replace the number in the second row by what
we get. To make it easy to do this mentally,
be sure to write -3 to the left of the 1st row
and 5 to the left ofthe 2nd row, so we can
easily do the work mentally:
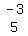
Notice that the second row can be divided through by -13,
so we stop and do that:
To get a 0 where the 1 in the middle on the top
row is, we mentally multiply each member of the
2nd row by -1 and mentally add it to 1 times the
corresponding number and replace the number in
the first row by what we get. To make it easy
to do this mentally, be sure to write -1 to the
left of the 2nd row and 1 to the left of the 1st
row, so we can easily do the work mentally:
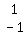
Now we just need to get a 1 where the 5 is. So
we divide the 1st row through by 5:
Now we interpret the matrix
as the sytem of equations:
or just
Edwin
