Question 167703This question is from textbook Algebra and Trigonometry
: In general, how do I find the logarithm of the answer
ex: evaluate 1776^53
I can get 53 Log 1776 = log x, but what is next?
This question is from textbook Algebra and Trigonometry
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1776^53
------------
Let x = 1776^53
log(x)= 53*log(1776)
log x = 53*3.24944...
---------------
10^(logx) = 10^(53*3.24944...)
x = 10^172.2203...
==================
Cheers,
Stan H.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Edwin's solution follows:
In general, how do I find the logarithm of the answer
ex: evaluate 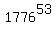
I can get  , but what is next? , but what is next?
You could get your calculator and find 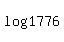 which is which is
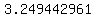 and then mutiply that by and then mutiply that by  to get to get
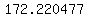 . However that won't get you any closer
to finding . However that won't get you any closer
to finding 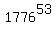 !
That's because calculators as a rule can only work
directly with numbers less than !
That's because calculators as a rule can only work
directly with numbers less than 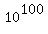 , "1 google".
You can't get , "1 google".
You can't get 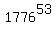 on a calculator directly because
that number is bigger than googol. Most calculators made today
can do anything but give an overflow error message for a google
and anything larger.
However you can get larger numbers indirectly on your calculator.
On my calculator I find that I can get on a calculator directly because
that number is bigger than googol. Most calculators made today
can do anything but give an overflow error message for a google
and anything larger.
However you can get larger numbers indirectly on your calculator.
On my calculator I find that I can get 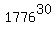 directly as
directly as  However when I try to get
However when I try to get  I get an overflow
error message.
We can break I get an overflow
error message.
We can break 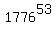 down this way: down this way:
 both of which can be
found on the calculator: both of which can be
found on the calculator:

 Then we can multiply those decimal parts,
Then we can multiply those decimal parts,  then add the exponents of ten and get
then add the exponents of ten and get  So therefore
So therefore
 However, that's not in scientific notation because
However, that's not in scientific notation because 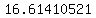 is not less than 10, so we write it in scientific notation as
is not less than 10, so we write it in scientific notation as
 , then substituting we have , then substituting we have
 or adding the exponents of ten:
or adding the exponents of ten:
 Notice that we could have broken
Notice that we could have broken 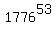 down in a number
of other ways, for example: down in a number
of other ways, for example:
 so
so
 .
And so we have, as above: .
And so we have, as above:
 There is a slight difference between the two. I would guess
that that latter is closer to the true value, but we could
safely round either answer to this:
There is a slight difference between the two. I would guess
that that latter is closer to the true value, but we could
safely round either answer to this:
 Edwin
Edwin
|
|
|