SOLUTION: The graph of f (x) = ax2 + bx + c passes through the points (1, k1), (2, k2), and (3, k3). Determine a, b, and c for (A) k1=-2, k2 = 1, k3 = 6 (B) k1 = 4, k2 = 3, k3=-2 (C) k1

Algebra ->  Matrices-and-determiminant -> SOLUTION: The graph of f (x) = ax2 + bx + c passes through the points (1, k1), (2, k2), and (3, k3). Determine a, b, and c for (A) k1=-2, k2 = 1, k3 = 6 (B) k1 = 4, k2 = 3, k3=-2 (C) k1      Log On


   

Question 167529: The graph of f (x) = ax2 + bx + c passes
through the points (1, k1), (2, k2), and (3, k3). Determine a,
b, and c for
(A) k1=-2, k2 = 1, k3 = 6
(B) k1 = 4, k2 = 3, k3=-2
(C) k1 = 8, k2=-5, k3 = 4
I attempted to solve as follows:
(A)-2= a + b + c
1= a - b + c
6= 4a + 2b +c
and entering this into a matrix, but it doesn't come out right.
What am I doing wrong?
Thank you!
Debi
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
The graph of f%28x%29+=+ax%5E2+%2B+bx+%2B+c passes
through the points (1, k1), (2, k2), and (3, k3). Determine a,
b, and c for

Plug x=1 in:
f%28x%29+=+ax%5E2+%2B+bx+%2B+c
f%281%29+=+a%281%29%5E2+%2B+b%281%29+%2B+c
f%281%29+=+a%281%29+%2B+b%281%29+%2B+c
f%281%29+=+a%2Bb%2Bc

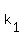Now since the graph passes through matrix%281%2C5%2C%22%28%22%2C1%2C%22%2C%22%2Ck%5B1%5D%2C%22%29%22%29
then f%281%29=k%5B1%5D, so substitute k%5B1%5D for f%281%29 in

f%281%29=a%2Bb%2Bc

or

a%2Bb%2Bc=k%5B1%5D

Plug x=2 in:
f%28x%29+=+ax%5E2+%2B+bx+%2B+c
f%282%29+=+a%282%29%5E2+%2B+b%282%29+%2B+c
f%282%29+=+a%284%29+%2B+b%282%29+%2B+c
f%282%29+=+4a%2B2b%2Bc

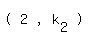Now since the graph passes through matrix%281%2C5%2C%22%28%22%2C2%2C%22%2C%22%2Ck%5B2%5D%2C%22%29%22%29
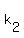then f%282%29=k%5B2%5D, so substitute k%5B2%5D for f%282%29 in

f%282%29=4a%2B2b%2Bc

Plug x=3 in:
f%28x%29+=+ax%5E2+%2B+bx+%2B+c
f%283%29+=+a%283%29%5E2+%2B+b%283%29+%2B+c
f%283%29+=+a%289%29+%2B+b%283%29+%2B+c
f%283%29+=+9a%2B3b%2Bc

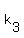Now since the graph passes through matrix%281%2C5%2C%22%28%22%2C3%2C%22%2C%22%2Ck%5B3%5D%2C%22%29%22%29
then f%283%29=k%5B3%5D, so substitute k%5B3%5D for f%283%29 in

f%283%29+=+9a%2B3b%2Bc

k%5B3%5D+=+9a%2B3b%2Bc or

9a%2B3b%2Bc=k%5B3%5D

So we have this system:


system%28a%2Bb%2Bc=k%5B1%5D%2C+4a%2B2b%2Bc=k%5B2%5D%2C+9a%2B3b%2Bc=k%5B3%5D%29

------------------------------------------------
(A) matrix%281%2C5%2Ck1=-2%2C%22%2C%22%2Ck2+=+1%2C%22%2C%22%2Ck3+=+6%29

the system

system%28a%2Bb%2Bc=k%5B1%5D%2C+4a%2B2b%2Bc=k%5B2%5D%2C+9a%2B3b%2Bc=k%5B3%5D%29

becomes

system%28a%2Bb%2Bc=-2%2C+4a%2B2b%2Bc=1%2C+9a%2B3b%2Bc=6%29

Solve this system and get matrix%281%2C5%2C+a=1%2C%22%2C%22%2C+b=0%2C+%22%2C%22%2C+c=-3%29

--------

(B) matrix%281%2C5%2Ck1=4%2C%22%2C%22%2Ck2+=+3%2C%22%2C%22%2Ck3+=+-2%29

the system

system%28a%2Bb%2Bc=k%5B1%5D%2C+4a%2B2b%2Bc=k%5B2%5D%2C+9a%2B3b%2Bc=k%5B3%5D%29

becomes

system%28a%2Bb%2Bc=4%2C+4a%2B2b%2Bc=3%2C+9a%2B3b%2Bc=-2%29

Solve this system and get matrix%281%2C5%2C+a=-2%2C%22%2C%22%2C+b=5%2C+%22%2C%22%2C+c=1%29

----------

(C) matrix%281%2C5%2Ck1=8%2C%22%2C%22%2Ck2+=+-5%2C%22%2C%22%2Ck3+=+4%29

the system

system%28a%2Bb%2Bc=k%5B1%5D%2C+4a%2B2b%2Bc=k%5B2%5D%2C+9a%2B3b%2Bc=k%5B3%5D%29

becomes

system%28a%2Bb%2Bc=8%2C+4a%2B2b%2Bc=-5%2C+9a%2B3b%2Bc=4%29

Solve this system and get matrix%281%2C5%2C+a=11%2C%22%2C%22%2C+b=-46%2C+%22%2C%22%2C+c=43%29

Edwin