Question 167514This question is from textbook Functions and Relations
: The 45degree 60degree 75degree triangle has angles in arithmetic sequence.
In triangle ABC, AB=1, angle A=45degrees, and angle B=60 degrees, without using a calculator how can I show these expressions?
a)the lengths of AC and BC
b)sin 75degrees, cos 75degrees, tan75degrees
c)sin 15degrees, cos 15degrees, tan 15degrees
This question is from textbook Functions and Relations
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll leave you the sketch, hopefully we can follow together.
In the triangle ABC, given:
 ; ;  ; ; 

Pardon me for the illustration below is just for reference --> NOT TO SCALE. So it will be easy for us to go along.
 ---> BLUE circle>>> ---> BLUE circle>>> ; GREEN Circle>>> ; GREEN Circle>>>  ; RED Circle>>> ; RED Circle>>>  . Also,BLUE LINE = . Also,BLUE LINE = ; GREEN LINE= ; GREEN LINE= ; RED LINE= ; RED LINE=
a)the lengths of AC and BC
In order to find  and and  with given data,w e draw a line from with given data,w e draw a line from  to line to line  and mark LINE and mark LINE  . See below: . See below:
 ---> BLACK Line= ---> BLACK Line=
We know  -------------> Eqn 1 >>>> as shown on the graph -------------> Eqn 1 >>>> as shown on the graph
We find  forms right triangle. By Trigo Functions: forms right triangle. By Trigo Functions:
Find first Line  ---> --->  ---> ---> ---------> Eqn 2: ---------> Eqn 2:
But,  --> -->  --------------> Eqn 3 --------------> Eqn 3
Subst. Eqn 3 in Eqn 2:
 ------------------> Eqn 4 ------------------> Eqn 4
.
Next, Line 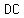 , On Angle , On Angle  : :

 -----------> Eqn 5 -----------> Eqn 5
Therefore, Via Eqn 1:
 ------------------> Eqn 6 ------------------> Eqn 6
*Note:  as per given as per given
.
Next, Line  =? =?



 ---------------> Eqn 7 ---------------> Eqn 7
.
b)sin 75degrees, cos 75degrees, tan75degrees
First  =?, =?,
On Right Triangle  with with  : :




Next,  =?, =?,




.
Next, 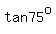 =? =?




.
c)sin 15degrees, cos 15degrees, tan 15degrees
We draw a line from  to to  as shown: as shown:
Mark Line 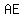 .See below: .See below:
 ----> We call it angle ----> We call it angle  from A --> E. from A --> E.
.
We solve for 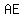 : :

 ------------> Eqn 8 ------------> Eqn 8
Next, 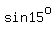 =? =?

 -------------------> Eqn 9 -------------------> Eqn 9
Next, 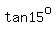 =? =?

Try to finish it off with what we've computed on the above EQUATIONS 1-9:
.
Thank you,
Jojo
|
|
|