|
Question 167399: Not sure if this is the right section but will someone please help.
Find the LCM of m^2-4m-5 and m^2+8m+7
Thanks
Found 2 solutions by gonzo, Electrified_Levi:
Answer by gonzo(654)   (Show Source):
You can put this solution on YOUR website! m^2 - 4m - 5 factors out to be (m+1) * (m-5)
m^2 + 89m + 7 factors out to be (m+1) * (m+7)
the common factors appears to be (m+1).
i would say that's your answer.
it's no different than finding out the least common multiplier of 9 and 12.
9 is 9*1 or 3*3 and 12 is 12*1 or 6*2 or 4*3.
LCM is 3
hope that helps.
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Not sure if this is the right section but will someone please help.
Find the LCM of  and 
Thanks
.
First, we can see if the two "numbers" can be factored
.
To find factors of something, you have to put the "m's" in paretheses ( since " =  ,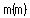
.
For , (m )(m ) , next we have to find all factors of (-5), and the factors have to add up to (-4), the middle term
.
Factors of (-5), (-5) and (1), (-1) and (5), now add each pair of factors
.
 ,
.
.
The first pair of factors add up to (-4), our middle term
.
We can put (-5) and (1) in our paretheses
.
(m )(m ) = (m - 5)(m + 1), if we used the FOIL method we would come up with our original equation
.
(m - 5)(m + 1) =  =  =  = 
.
(Remember the negative and positive signs,  =  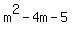(Our answers are true)
.
The factors for our first "number" = (m - 5)(m + 1)
.
Now we will find the factors of the second equation,
.
First, we put the "m's" in parentheses, (m )(m )
.
Remember, the factors of "7" add up to the middle term "8"
.
Factors of "7", (-7) and (-1), (1) and (7)
.
Adding them we get,
.
.
.
The second factors work. We can put the factors in the parentheses
.
(m + 1)(m + 7), If we used the FOIL method,
.
(m + 1)(m + 7) =  =  =  = 
.
Remember signs,  =  ( our factors our true )
.
Our factors for our second "number" = (m + 1)(m + 7)
.
We can now put the factored equations side by side
.
Equation (1), (m - 5)(m + 1)
.
Equation (2), (m + 1)(m + 7)
.
To find the LCM, we count all the DIFFERENT factors
.
All factors put together = (m - 5)(m + 1)(m + 1)(m + 7),
.
There are three different factors, (m - 5)(m + 1)(m + 7), ( both numbers have (m + 1) in common, so we only count that factor once )
.
The LCM would then be  , if we expanded it, 
.
The LCM =
.
Hope I helped, Levi
|
|
|
| |
