SOLUTION: Please find all integers b for which a^2 + ba - 50 can be factored.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Please find all integers b for which a^2 + ba - 50 can be factored.      Log On


   

Question 167220This question is from textbook Introductory Algebra
: Please find all integers b for which a^2 + ba - 50 can be factored. This question is from textbook Introductory Algebra

Found 2 solutions by vleith, Edwin McCravy:
Answer by vleith(2983) About Me  (Show Source):
You can put this solution on YOUR website!
To solve this, find all the two pair factors of 50
50 * -1 and -50 * 1
25 * -2 and -25 * 2
5 * -10 and -5 * 10
For each pair, find the value of b that results from using that pair
Example (a + 50)(a -1) = a^2 +49a - 50 --> b=49
(a - 50)(a + 1) = a^2 -49a - 50 --> b=-49
Do the same for the other 4 pairs to find the other values of b

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Edwin's solution:
Please find all integers b for which 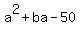a%5E2+%2B+ba+-+50 can be factored.

The only ways to factor 50 into the product of
two integers are 1x50, 2x25, and 5x10,

Therefore any factorization of 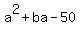a%5E2+%2B+ba+-+50 must be one of these:

%28a%2B1%29%28a-50%29=a%5E2-49a-50, so b=-49
%28a-1%29%28a%2B50%29=a%5E2%2B49a-50, so b=49
%28a%2B2%29%28a-25%29=a%5E2-23a-50, so b=-23
%28a-2%29%28a%2B25%29=a%5E2%2B23a-50, so b=23
%28a%2B5%29%28a-10%29=a%5E2-5a-50, so b=-5
%28a-5%29%28a%2B10%29=a%5E2%2B5a-50, so b=5

So there are 6 possible values for b.
They are

 ±49, ±23, ±5

Edwin