Question 166504: These will be the last questions. Please help
1. List all of the possible rational zeros of f(x)=3x^5-7x^3+2x-15.
2. State the number of positive real zeros, negative real zeros, and imaginary zeros for g(x)=9x^3-7x^2+10x-4.
I must show my work. No textbook. Have been absent from school and have a big test on Monday. Need to know how to do these for the test.
Thanks
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
Any rational zero can be found through this equation
 where p and q are the factors of the last and first coefficients where p and q are the factors of the last and first coefficients
So let's list the factors of -15 (the last coefficient):

Now let's list the factors of 3 (the first coefficient):

Now let's divide each factor of the last coefficient by each factor of the first coefficient

Now simplify
These are all the distinct rational zeros of the function that could occur

# 2
Now let's use Descartes Rule of Signs to find the number of positive, negative,and imaginary zeros.
First count the sign changes of 
From 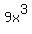 to to  , there is a sign change from positive to negative , there is a sign change from positive to negative
From  to to  , there is a sign change from negative to positive , there is a sign change from negative to positive
From  to to  , there is a sign change from positive to negative , there is a sign change from positive to negative
So there are 3 sign changes for the expression  . .
So there are 3 or 1 positive zeros
So if there are 3 positive zeros, then there will be NO imaginary zeros (since there a total of 3 zeros)
Or...
If there is only 1 positive zero, then there will be 2 imaginary zeros.
------------------------------------------------
 Now let's replace each Now let's replace each  with with 
 Simplify Simplify
Now let's count the sign changes of 
From 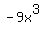 to to  , there is no change in sign , there is no change in sign
From  to to 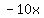 , there is no change in sign , there is no change in sign
From 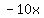 to to  , there is no change in sign , there is no change in sign
So there are no sign changes for the expression 
So there are 0 negative zeros
==========================================
Answer:
So here are the possibilities:
3 positive zeros, 0 negative zeros, and 0 imaginary zeros
Or...
1 positive zero, 0 negative zeros, and 2 imaginary zeros
|
|
|