SOLUTION: I'm not sure if this is the right section. I have two question's with no textbook. 1. identify the vertex, axis of symmetry, and direction of opening for y=2(x+3)^2-5. 2. Writ

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I'm not sure if this is the right section. I have two question's with no textbook. 1. identify the vertex, axis of symmetry, and direction of opening for y=2(x+3)^2-5. 2. Writ      Log On


   

Question 166497: I'm not sure if this is the right section. I have two question's with no textbook.
1. identify the vertex, axis of symmetry, and direction of opening for y=2(x+3)^2-5.
2. Write y=-4x^2+8x-1 in vertex form.
I must show my work.
Please HELP!!!
Thanks
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
# 1


y=2%28x%2B3%29%5E2-5 Start with the given equation


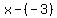
y=2%28x-%28-3%29%29%5E2-5 Rewrite x%2B3 as x-%28-3%29


Now the equation above is in vertex form y=a%28x-h%29%5E2%2Bk where (h,k) is the vertex and 'a' determines which direction it opens up. In this case, a=2, h=-3 and k=-5.


So because a%3E0, this tells us that the parabola opens up. Also, since h=-3 and k=-5, the vertex is (-3,-5). Finally, the axis of symmetry is simply the x-coordinate of the vertex. So the axis of symmetry is x=-3


=======================
Answer:

Direction of opening: up
Vertex: (-3,-5)
Axis of Symmetry: x=-3





# 2



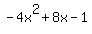-4x%5E2%2B8x-1 Start with the right side of the given equation.


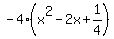-4%28x%5E2-2x%2B1%2F4%29 Factor out the x%5E2 coefficient -4. This step is very important: the x%5E2 coefficient MUST be equal to 1.


Take half of the x coefficient -2 to get -1. In other words, %281%2F2%29%28-2%29=-1.


Now square -1 to get 1. In other words, %28-1%29%5E2=%28-1%29%28-1%29=1


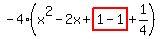-4%28x%5E2-2x%2Bhighlight%281-1%29%2B1%2F4%29 Now add and subtract 1 inside the parenthesis. Make sure to place this after the "x" term. Notice how 1-1=0. So the expression is not changed.


-4%28%28x%5E2-2x%2B1%29-1%2B1%2F4%29 Group the first three terms.


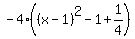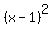-4%28%28x-1%29%5E2-1%2B1%2F4%29 Factor x%5E2-2x%2B1 to get %28x-1%29%5E2.


-4%28%28x-1%29%5E2-3%2F4%29 Combine like terms.


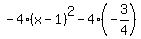-4%28x-1%29%5E2-4%28-3%2F4%29 Distribute.


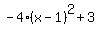-4%28x-1%29%5E2%2B3 Multiply.


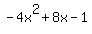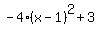So after completing the square, -4x%5E2%2B8x-1 transforms to -4%28x-1%29%5E2%2B3. So -4x%5E2%2B8x-1=-4%28x-1%29%5E2%2B3.

================================
Answer:

So the answer is y=-4%28x-1%29%5E2%2B3 which is now in vertex form y=a%28x-h%29%5E2%2Bk where a=-4, h=-1, and k=3