the sum of the squares of six consecutive integers is 1111. what are the integers and what is the problem solving strategy?
Let consecutive the integers be  ,
,  ,
,  ,
,  ,
,  , and
, and  Then we have the equation:
Then we have the equation:


 Collect terms:
Collect terms:

 Divide through by 6:
Divide through by 6:
 Factor:
Factor:
 Use the zero factor property:
Use the zero factor property:
 So there are two solutions:
If
So there are two solutions:
If  , then the consecutive integers are
, then the consecutive integers are
 ,
,  ,
,  ,
,  ,
,  , and
, and  or
or
 ,
, 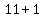 ,
, 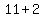 ,
, 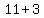 ,
, 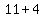 , and
, and 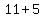 or
or
 ,
,  ,
,  ,
,  ,
,  , and
, and  and if
and if  , then the consecutive integers are
, then the consecutive integers are
 ,
,  ,
,  ,
,  ,
,  , and
, and  or
or
 ,
, 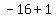 ,
, 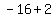 ,
, 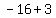 ,
, 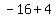 , and
, and 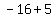 or
or
 ,
,  ,
,  ,
,  ,
,  , and
, and  Edwin
Edwin