SOLUTION: Hi, Can you help? . In my algebra book, It says that if the degree of the numerator is more than the denominator ( by more than one degree ), it does not have any horizontal asym

Algebra ->  Rational-functions -> SOLUTION: Hi, Can you help? . In my algebra book, It says that if the degree of the numerator is more than the denominator ( by more than one degree ), it does not have any horizontal asym      Log On


   

Question 165725: Hi, Can you help?
.
In my algebra book, It says that if the degree of the numerator is more than the denominator ( by more than one degree ), it does not have any horizontal asymptotes, is this true?
.
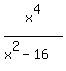+x%5E4%2F%28x%5E2-16%29+ only has Vertical asymptotes of +x+=+4+, and +x+=+-4+
.
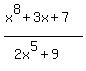+%28x%5E8+%2B+3x+%2B+7%29%2F%282x%5E5+%2B+9%29+ would only have Vertical asymptotes
.
If the degrees are the same, the Horizontal asymptotes would be the leading coeffiecients, is this true?
.
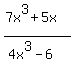+%287x%5E3+%2B+5x%29%2F%284x%5E3+-+6%29+ would have Horizontal asymptotes of +y+=+7%2F4+
.
If the degree of the numerator is smaller than the denominator, than the Horizontal asymptotes would always be +y+=+0+, is this true?
.
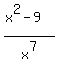+%28x%5E2-9%29%2Fx%5E7+, would have a Horizontal Asymtote of +y+=+0+
.
If the numerator is only one degree more than the denominator, it doesn't have a Horizontal Asymptote, but it has an Oblique Asymptote (unless it is exactly divisible), is this true?
.
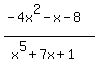
+%28x%5E6+%2B3x%5E2+-+8%29%2F%28x%5E5%2B7x%2B1%29+, would have an Oblique Asymptote of +y+=+x+, (It has a remainder of +%28-4x%5E2-x-8%29%2F%28x%5E5%2B7x%2B1%29+
.
Am I correct with all these examples? ( I would appreciate it if I could have an answer as soon as possible )
.
Thanks ahead of time,Levi
Answer by MRperkins(300) About Me  (Show Source):
You can put this solution on YOUR website!
Wow! You make it easy for us when you write everything out like you did. Thank you for putting the time and effort into doing this.
.
Yes, your examples are correct.
.
MRperkins