Question 165121: 1. A rectangular garden has dimensions of 18 feet by 13 feet. A gravel path of uniform width is to be built around the garden. How wide can the path be if there is enough gravel for 516 square feet?
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! Draw a diagram of the problem -- it'll help you see how to solve it.
.
If you do, the "inner rectangle" represents the garden while the "outer rectangle" (bordered by the outside edge of the gravel path).
.
"outer rectangle" - "inner rectangle" = "area of gravel path"
.
Let x = width of gravel path
.
"outer rectangle" then is:
(2x+18)(2x+13)
= 4x^2 + 26x + 36x + 234
= 4x^2 + 62x + 234
.
"Inner rectangle" is:
18 * 13 = 234
.
Now, instead of:
"outer rectangle" - "inner rectangle" = "area of gravel path"
we have:
(4x^2 + 62x + 234) - 234 = 516
4x^2 + 62x = 516
4x^2 + 62x - 516 = 0
2x^2 + 31x - 258 = 0
Since, it is difficult to factor, use the quadratic equation. It will yield:
x = {6, -21.5}
.
Since the negative solution does not make sense, throw it out leaving:
x = 6 feet (width of gravel path)
.
Details of quadratic:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=3025 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 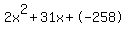 can be factored: can be factored:

Again, the answer is: 6, -21.5.
Here's your graph:
 |
|
|
|