SOLUTION: 64.) Find all real solutions to each equation. {{{x^2+x+ sqrt(x^2+x)-2=0}}}

Put parentheses around the first two terms:



Notice that 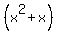 occurs in two places, so let the
variable part of the middle term, in this case the whole
middle term, 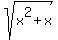be equal to the letter .

That is to say we are letting 



Now we square both sides:





So we substitute  for 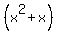 in the original 
equation, and  for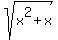 



becomes the much simpler looking equation:



Factoring:



Using the zero-factor property,

   

So now we have to substitute back.





We can tell immediately that  has no
solution because square roots when written as a radical
are never negative, so that square root on the left
could not equal to -2 on the right.

So we solve



Square both sides:

 













Edwin