Question 164959This question is from textbook Elementary and Intermediate
: 14.) Solve each equation by using the quadratic formula
-8q^2-2q+1=0
This question is from textbook Elementary and Intermediate
Found 2 solutions by checkley77, Electrified_Levi:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! -8q^2-2q+1=0

q=(2+-sqrt[-2^2-4*-8*1])/2*-8
q=(2+-sqrt4+32)/-16
q=(2+-sqrt36)/-16
q=(2+-6)/-16
q=(2+6)/-16
q=(8/-16
q=-1/2 answer.
q=(2-6)/-16
q=-4/-16
q=1/4 answer.
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
14.) Solve each equation by using the quadratic formula

.
First we have to but the equation in the standard form 
.
It is already in that form. (x is replaced with q)
.
 , , 
.
A = (-8)
B = (-2)
C = 1
.
We have to know the quadratic equation, which is
.

.
We can replace A with (-8), B with (-2), C with "1"
.
 = =  = =  = =  = =  = = 
.
There are two answers that "q" can equal ( + 6, - 6 )
.
 = =  = = 
.
 = =  = = 
.
q can be 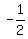 , and , and 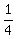
.
You can check by replacing "q" with " ", and " ", and " " in the original equation, " in the original equation, 
.
q = 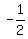 , ,  = =  = =  = =  = =  = =  (True) (True)
.
q =  , ,  = =  = =  = =  = =  = =  = =  (True) (True)
.
q = 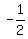
.
q = 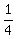
.
Here is the graph of the equation
.

.
Where the curved line crosses the x axis, are the solutions to the equation
.
The curved line crosses where "q"(or "x") = 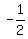 , it also crosses the x axis where "q"(or "x") = , it also crosses the x axis where "q"(or "x") = 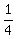
.
The two solutions are
.
q = 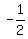
.
q = 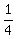
.
Hope I helped, Levi
|
|
|