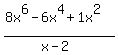 First write that numerator putting in zero placeholders:
First write that numerator putting in zero placeholders:
 List only those coefficients in that order:
8 0 -6 0 1 0 0
Draw a line on the left and underneath skipping
a line:
|8 0 -6 0 1 0 0
|
-------------------------
Change the sign of the second term of
List only those coefficients in that order:
8 0 -6 0 1 0 0
Draw a line on the left and underneath skipping
a line:
|8 0 -6 0 1 0 0
|
-------------------------
Change the sign of the second term of  , which is
, which is  to
to 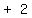 Write 2 left of the line:
2|8 0 -6 0 1 0 0
|
-------------------------
Bring the 8 down below the bottom line:
2|8 0 -6 0 1 0 0
|
-------------------------
8
Multiply the 8 by the 2, getting 16, so write
16 diagonally above and to the right of the
8 above the line and underneth the first 0 in
top row:
2|8 0 -6 0 1 0 0
| 16
-------------------------
8
Add the 0 and the 16, getting 16, and put 16 at
the bottom to the right of the bottom 8 and
underneath the line below
Write 2 left of the line:
2|8 0 -6 0 1 0 0
|
-------------------------
Bring the 8 down below the bottom line:
2|8 0 -6 0 1 0 0
|
-------------------------
8
Multiply the 8 by the 2, getting 16, so write
16 diagonally above and to the right of the
8 above the line and underneth the first 0 in
top row:
2|8 0 -6 0 1 0 0
| 16
-------------------------
8
Add the 0 and the 16, getting 16, and put 16 at
the bottom to the right of the bottom 8 and
underneath the line below  .
2|8 0 -6 0 1 0 0
| 16
-------------------------
8 16
Multiply that 16 at the bottom time the 2 at the far
let, getting 32. Place that diagonally above and to
the right of the 16, like this:
2|8 0 -6 0 1 0 0
| 16 32
-------------------------
8 16
Now add -6 and 32, getting 26, and place that under
the 32, like this:
2|8 0 -6 0 1 0 0
| 16 32
-------------------------
8 16 26
--
Multiply that 26 at the bottom time the 2 at the far
let, getting 52. Place that diagonally above and to
the right of the 26, like this:
2|8 0 -6 0 1 0 0
| 16 32 52
-------------------------
8 16 26
Now add 0 and 52, getting 52, and place that under
the 52, like this:
2|8 0 -6 0 1 0 0
| 16 32 52
-------------------------
8 16 26 52
Multiply that 52 at the bottom time the 2 at the far
let, getting 104. Place that diagonally above and to
the right of the 52, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104
-------------------------
8 16 26 52
Now add 0 and 104, getting 105, and place that under
the 104, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104
-------------------------
8 16 26 52 105
Multiply that 105 at the bottom time the 2 at the far
let, getting 210. Place that diagonally above and to
the right of the 52, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210
-------------------------
8 16 26 52 105
Now add 0 and 210, getting 210, and place that under
the 210, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210
-------------------------
8 16 26 52 105 210
Multiply that 210 at the bottom time the 2 at the far
let, getting 420. Place that diagonally above and to
the right of the 210, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210 420
-------------------------
8 16 26 52 105 210
Now add 0 and 420, getting 420, and place that under
the 420, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210 420
-------------------------
8 16 26 52 105 210 420
Now we must interpret that line of numbers across the
bottom.
The largest exponent in the original numerator,
.
2|8 0 -6 0 1 0 0
| 16
-------------------------
8 16
Multiply that 16 at the bottom time the 2 at the far
let, getting 32. Place that diagonally above and to
the right of the 16, like this:
2|8 0 -6 0 1 0 0
| 16 32
-------------------------
8 16
Now add -6 and 32, getting 26, and place that under
the 32, like this:
2|8 0 -6 0 1 0 0
| 16 32
-------------------------
8 16 26
--
Multiply that 26 at the bottom time the 2 at the far
let, getting 52. Place that diagonally above and to
the right of the 26, like this:
2|8 0 -6 0 1 0 0
| 16 32 52
-------------------------
8 16 26
Now add 0 and 52, getting 52, and place that under
the 52, like this:
2|8 0 -6 0 1 0 0
| 16 32 52
-------------------------
8 16 26 52
Multiply that 52 at the bottom time the 2 at the far
let, getting 104. Place that diagonally above and to
the right of the 52, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104
-------------------------
8 16 26 52
Now add 0 and 104, getting 105, and place that under
the 104, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104
-------------------------
8 16 26 52 105
Multiply that 105 at the bottom time the 2 at the far
let, getting 210. Place that diagonally above and to
the right of the 52, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210
-------------------------
8 16 26 52 105
Now add 0 and 210, getting 210, and place that under
the 210, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210
-------------------------
8 16 26 52 105 210
Multiply that 210 at the bottom time the 2 at the far
let, getting 420. Place that diagonally above and to
the right of the 210, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210 420
-------------------------
8 16 26 52 105 210
Now add 0 and 420, getting 420, and place that under
the 420, like this:
2|8 0 -6 0 1 0 0
| 16 32 52 104 210 420
-------------------------
8 16 26 52 105 210 420
Now we must interpret that line of numbers across the
bottom.
The largest exponent in the original numerator,
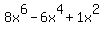 is 6. So we subtract 1 from
6 and get 5.
Then the first number on the bottom row, 8, will be the
coefficient of
is 6. So we subtract 1 from
6 and get 5.
Then the first number on the bottom row, 8, will be the
coefficient of 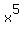 , and
, and 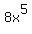 wil be the
first term of the quotient.
Then the second number on the bottom row, 16, will be the
coefficient of
wil be the
first term of the quotient.
Then the second number on the bottom row, 16, will be the
coefficient of 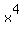 Then the third number on the bottom row, 26, will be the
coefficient of
Then the third number on the bottom row, 26, will be the
coefficient of  Then the fourth number on the bottom row, 52, will be the
coefficient of
Then the fourth number on the bottom row, 52, will be the
coefficient of  Then the fifth number on the bottom row, 105, will be the
coefficient of
Then the fifth number on the bottom row, 105, will be the
coefficient of 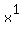 Then the sixth number on the bottom, 210, will be the
constant term, the last term of the quotient.
Then the seventh number of the bottom row, 420, is the very
last one. So it is different. It is the remainder that would
have been gotten if we had done the problem by long division.
It will be placed over the divisor
Then the sixth number on the bottom, 210, will be the
constant term, the last term of the quotient.
Then the seventh number of the bottom row, 420, is the very
last one. So it is different. It is the remainder that would
have been gotten if we had done the problem by long division.
It will be placed over the divisor  and added to
the quotient. So the answer is
and added to
the quotient. So the answer is
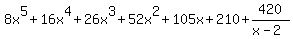 Edwin
Edwin