Question 164532This question is from textbook elementary and intermediate algebra
: I am having trouble getting started on these problems. Can someone please help?
Thank you in advance. Also, I may be making this too hard. Should I be factoring before I try to solve?
1. Determine whether the following equations have a solution or not? Justify your answer.
a) x2 + 6x - 7 = 0
b) z2 + z + 1 = 0
c) (3)1/2y2 - 4y - 7(3)1/2 = 0
d) 2x2 - 10x + 25 = 0
e) 2x2 - 6x + 5 = 0
f) s2 - 4s + 4 = 0
g) 5/6x2 - 7x - 6/5 = 0
h) 7a2 + 8a + 2 = 0
2. If x = 1 and x = -8, then form a quadratic equation.
This question is from textbook elementary and intermediate algebra
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll do the first two to get you started
For all of these problems, you need to use the discriminant formula  and you will get these possible solutions: and you will get these possible solutions:
If D>0 (ie the discriminant is positive), then you will have 2 real solutions,
If D=0, then you will have only 1 real solution, or
If D<0 (ie the discriminant is negative), then you will have 2 complex solutions (ie you will have NO real solutions).
a)
From  we can see that we can see that  , ,  , and , and 
 Start with the discriminant formula. Start with the discriminant formula.
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get 
 Multiply Multiply 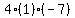 to get to get 
 Rewrite Rewrite  as as 
 Add Add  to to 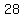 to get to get 
Since the discriminant is greater than zero, this means that there are two real solutions.
b)
From  we can see that we can see that  , ,  , and , and 
 Start with the discriminant formula. Start with the discriminant formula.
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get 
 Multiply Multiply  to get to get 
 Subtract Subtract  from from  to get to get 
Since the discriminant is less than zero, this means that there are two complex solutions. In other words, there are no real solutions.
|
|
|