Question 164168: $1.65 is made up of pennies, nickels, and dimes. Half of the coins are nickels. List a set of coins that will solve the problem including why only the set of coins you chose worked in this situation. Remember you are communication information to some one who may have no idea what you are talking about, so the more information you give, the better off you will be. Use proper grammar and complete sentences in your explanation
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll just work the problem for you. You'll have to
write it up using complete sentences and proper grammar,
and filling in your own explanations.
Let p = the number of pennies
Let n = the number of nickels
Let d = the number of dimes
We have the equation:
 or multiplying through by 100,
or multiplying through by 100,
 Since half the coins are nickels, we have
Since half the coins are nickels, we have


 We have the system:
We have the system:
 Substituting
Substituting 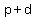 for for  in the first equation in the first equation


 Divide through by 3:
Divide through by 3:


 Since the left side is even,
the right side must be even also,
and positive. Therefore
Since the left side is even,
the right side must be even also,
and positive. Therefore 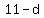 must be even and positive, too,
Therefore d must be odd and no more
than 11.
Therefore there are 6 possibilities:
d = 1, 3, 5, 7, 9, or 11
If
must be even and positive, too,
Therefore d must be odd and no more
than 11.
Therefore there are 6 possibilities:
d = 1, 3, 5, 7, 9, or 11
If  , then , then
 becomes becomes



 Substituting
Substituting  and and  into
into





 So one possibility is
So one possibility is
 , ,  , ,  -------
If
-------
If  , then , then
 becomes becomes



 Substituting
Substituting  and and  into
into





 So another possibility is
So another possibility is
 , ,  , ,  -----------------
If
-----------------
If  , then , then
 becomes becomes



 Substituting
Substituting  and and  into
into





 So another possibility is
So another possibility is
 , ,  , ,  -------------
If
-------------
If  , then , then
 becomes becomes



 Substituting
Substituting  and and  into
into





 So another possibility is
So another possibility is
 , ,  , ,  -------------
If
-------------
If  , then , then
 becomes becomes



 Substituting
Substituting  and and  into
into





 So another possibility is
So another possibility is
 , ,  , ,  -------------
If
-------------
If  , then , then
 becomes becomes



 Substituting
Substituting  and and  into
into




 So another possibility is
So another possibility is
 , ,  , ,  -------------
So all the 6 possibilities are
0 pennies, 11 nickels, 11 dimes, 22 coins, half of which are 11 nickels.
5 pennies, 14 nickels, 9 dimes, 28 coins, half of which are 14 nickels.
10 pennies, 17 nickels, 7 dimes, 34 coins, half of which are 17 nickels.
15 pennies, 20 nickels, 5 dimes, 40 coins, half of which are 20 nickels.
20 pennies, 23 nickels, 3 dimes, 46 coins, half of which are 23 nickels.
25 pennies, 26 nickels, 1 dimes, 52 coins, half of which are 26 nickels.
Edwin
-------------
So all the 6 possibilities are
0 pennies, 11 nickels, 11 dimes, 22 coins, half of which are 11 nickels.
5 pennies, 14 nickels, 9 dimes, 28 coins, half of which are 14 nickels.
10 pennies, 17 nickels, 7 dimes, 34 coins, half of which are 17 nickels.
15 pennies, 20 nickels, 5 dimes, 40 coins, half of which are 20 nickels.
20 pennies, 23 nickels, 3 dimes, 46 coins, half of which are 23 nickels.
25 pennies, 26 nickels, 1 dimes, 52 coins, half of which are 26 nickels.
Edwin
|
|
|