Question 164077This question is from textbook elementary and intermediate algebra
: Please help me understand what this problem is asking and how do I determine what equation to use when solving? Are there any key words that will tell me what equation I should use?Thanks for your help?
What three techniques can be used to solve a quadratic equation? Demonstrate these techniques on the equation "12x2 - 10x - 42 = 0".
This question is from textbook elementary and intermediate algebra
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three ways to solve a quadratic equation:
1) Use the "quadratic formula" and this will always work:
2) "Completing the square", this will always work too.
3) "Factoring", this will work only if the equation is factorable.
Which one to use? Your experience in solving quadratic equations is probably the best guide, but I always try factoring first and, if I'm unable to factor, then I'll use the formula, but sometimes, depending on what the problem is asking for, I'll use completing the square.
Let's try these methods on your equation:
1) The quadratic formula.
To use this, your equation should be written in the "standard format":
 and, in this case, it already is. and, in this case, it already is.
 Here, a = 12, b = -10, and c = -42. Apply the formula: Here, a = 12, b = -10, and c = -42. Apply the formula:
 Simplify this. Simplify this.


 or or 
 or or 
2) Completing the square.
 First, divide through by 12 to get the First, divide through by 12 to get the  coefficient equal to 1. coefficient equal to 1.
 Now add Now add  to both sides. to both sides.
 Complete the square in x by adding the square of half the x-coefficient, that's ( Complete the square in x by adding the square of half the x-coefficient, that's ( ) to both sides. ) to both sides.
 Rewrite the left side as the square of the binomial: Rewrite the left side as the square of the binomial: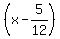 and simplify the right side. and simplify the right side.

 Now take the square root of both sides. Now take the square root of both sides.
 or or  Add Add 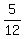 to both sides. to both sides.
 or or 
 or or 
 or or 
3) Factoring.
 Factor the trinomial: Factor the trinomial:
 Apply the zero product rule: Apply the zero product rule:
 or or 
If  then then  so that so that  or or 
If  then then  so that so that  or or 
|
|
|