Question 164005: Prove that the area of a circular sector of radius r with central angle theta is  , where theta is measured in radians. , where theta is measured in radians.
The following is what I've come up with so far, am I on the right track?
I can tell that a circular sector looks similar to a triangle with an arc replacing its flat base. The area of a triangle is computed using A=1/2bh. Therefore:
h=r
b=s=r(theta)
A=(1/2)rr(theta) which is simplified to 
Found 2 solutions by Alan3354, Dr.E:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Prove that the area of a circular sector of radius r with central angle theta is , where theta is measured in radians.
The following is what I've come up with so far, am I on the right track?
I can tell that a circular sector looks similar to a triangle with an arc replacing its flat base. The area of a triangle is computed using A=1/2bh. Therefore:
h=r
b=s=r(theta)
A=(1/2)rr(theta) which is simplified to 
--------------------
 (You left out the theta) (You left out the theta)
What you've done is the correct approach. This can be done as a limit, or by integral calculus, which is essentially the same thing. I don't know if your instructor would accept an integration, tho, it depends on the level of your class.
Answer by Dr.E(1)  (Show Source): (Show Source):
You can put this solution on YOUR website! --------------------------------------------------------------------------------
Dr.E's Solution:
Hello!
I would stray away from the calculus proofs by integration and other such mathematical inductions until you reach those classes or are told to use such methods in calculus to solve this problem. Since this is an algerbra tutoring website, I doubt the need to do so. Let me know if you need it.
Remember from your earlier studies that the Area of a Circle is = 
The area of the sector of a circle is proportional its central sector.
In simpler terms, if I said that I wanted you to find  ths of the circle, you would simply: ths of the circle, you would simply: 
Same if I asked you to find  , circle: , circle: 
In other terms, we could have said that  of the circle, in terms of the central angle, is of the circle, in terms of the central angle, is 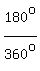 or or 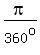 of the (full of the (full  ) )  or or 
Thus, we can infer that given a central angle labeled 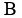 , would simply be , would simply be 
Put everything in terms of radians ( ), ), 
=  (then the (then the  's cancel out) 's cancel out)
= 
Thus, by using the sector area formula of a circle, which you can derive from the area of a circle, unless your teacher said you have to derive the area of a circle, which would require your knowledge in integral calculus (which I highly doubt) then this is a valid proof for algebra and geometry.
If you have any more questions, don't hesitate to ask!
Have fun with your algebra!
Dr.E
|
|
|