|
Question 163673: an examination paper consists of 40 questions.
5 marks are given for each correct answer.
3 marks are deducted for each incorrect answer.
Kenny answered all 40 questions, getting x correct and y incorrect.
His total score for the examination was 56 marks.
(i)Write two equations to represent the above information.
(ii)Solve these equations to find out how many questions answered correctly
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
an examination paper consists of 40 questions.
5 marks are given for each correct answer.
3 marks are deducted for each incorrect answer.
Kenny answered all 40 questions, getting x correct and y incorrect.
His total score for the examination was 56 marks.
(i)Write two equations to represent the above information.
(ii)Solve these equations to find out how many questions answered correctly
.
First we have to find the two equations.
.
First equation - Since there are 40 questions, both the wrong answered questions, as well as the right answered questions add up to 40 questions
.
If "x" is the number of correct answers, "y" is the number of wrong answers we can add these together and they will equal 40, our first equation is equal to 
.
 is our first equation is our first equation
.
Second equation - 5 marks are given for each correct answer.
3 marks are deducted for each incorrect answer. His total score for the examination was 56 marks.
.
If he answered "x" number of problems right, he gets 5 marks for each problem that is right. To get the number of marks for right answers, you would multiply the number of marks for one right answer(5) by the number of right answers ("x"). So the number of marks for right answers would be 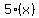 or or 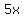 . If he answered "y" number of problems wrong, he gets 3 marks taken off for each wrong answer. To find the number of marks for wrong answers, you multiply the number of marks for one wrong answer (3) by the number of wrong answers ("y"). The number of marks for wrong answers would be . If he answered "y" number of problems wrong, he gets 3 marks taken off for each wrong answer. To find the number of marks for wrong answers, you multiply the number of marks for one wrong answer (3) by the number of wrong answers ("y"). The number of marks for wrong answers would be 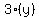 or or 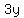 , these marks are taken away from the right answer marks (5x), if you take the marks away, his total marks would be 56, to find the equation, take the number of "wrong" marks ( 3y) from the "right" marks (5x) and that will equal 56, the equation would be , these marks are taken away from the right answer marks (5x), if you take the marks away, his total marks would be 56, to find the equation, take the number of "wrong" marks ( 3y) from the "right" marks (5x) and that will equal 56, the equation would be 
.
 is the second equation, we found the two equations is the second equation, we found the two equations
.
Equation 1 = 
.
Equation 2 = 
.
To solve for "x" and "y", there are several methods you can use. We will use the easiest method for solving any system of equations.
.
First solve for a letter in both equations, doesn't matter which one, usually the easiest. We will solve for "x" in both equations
.
Equation 1,  , ,
.
To solve for "x" we will move "y" to the right side.
.
 = =  = =  , rearranging , rearranging 
.
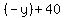 is our first answer is our first answer
.
Second equation, 
.
To start solving we will move (-3y) to the right side
.
 = =  = =  , rearranging , rearranging 
.
To find "x" we will divide each side by "5"
.
 = =  = = 
.
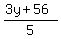 is our second answer, the two answers will equal each other, since both of them equal "x" is our second answer, the two answers will equal each other, since both of them equal "x"
.
We can put them both in an equation, and then solve for "y"
.
 = =  , now all you do is solve for "y". , now all you do is solve for "y".
.
We can cross multiply
.
 = =  = =  = =  , If we rearrange the first part it becomes , If we rearrange the first part it becomes 
.
We can use the distributive property to solve for "y" even more.
.
 = =  = =  = = 
.
We will move (-5y) to the right side
.
 = =  = =  , to solve it even more we will move the "56" to the left side , to solve it even more we will move the "56" to the left side
.
 = =  = =  , rearranging we get , rearranging we get 
.
To solve for "y" we need to divide each side by "8"
.
 = =  = = 
.
We found "y",  , we can check by replacing "y" in the equation, , we can check by replacing "y" in the equation, 
.
Replacing "y" with "18",  = =  = =  = =  = =  (True) (True)
.
To find "x" we will replace "y" with "18" in one of the original equations
.
Equation 1 = 
.
Equation 2 =  , we will use the first equation , we will use the first equation
.
Replacing "y" with "18",  = =  = = 
.
To find "x" we will move "18" to the right side
.
 = =  = = 
.
We found "x", 
.
Our two answers are
.

.

.
We can check our answers by replacing "x" with "22", "y" with "18" in both of our original equations
.
Replacing "x" with "22", "y" with "18"
.
Equation 1 =  = =  = =  (True) (True)
.
Equation 2 =  = =  = =  = =  (True) (True)
.
 , ( Since "x" was the number of problems he got right, he got 22 problems right ) , ( Since "x" was the number of problems he got right, he got 22 problems right )
.
 , ( Since "y" was the number of problems he got wrong, he got 18 problems wrong ) , ( Since "y" was the number of problems he got wrong, he got 18 problems wrong )
.
He got 22 problems right
.
He got 18 problems wrong
.
Hope I helped, Levi
|
|
|
| |