SOLUTION: Find the maximum value of F=7y-4x subjet to x+y<or=8 4x-3y<or=12 x>or=0 y>or=0

Algebra ->  Matrices-and-determiminant -> SOLUTION: Find the maximum value of F=7y-4x subjet to x+y<or=8 4x-3y<or=12 x>or=0 y>or=0      Log On


   

Question 163622This question is from textbook College Algebra
: Find the maximum value of F=7y-4x subjet to
x+y 4x-3y x>or=0
y>or=0 This question is from textbook College Algebra

Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
First let's graph the feasible region.
x%2By%3C=8
4x-3y%3C=12
x%3E=0
y%3E=0
+graph%28+300%2C+300%2C+-2%2C+10%2C+-2%2C+5%2C+8-x%2C+%284x-12%29%29+
The feasible region is the triangle bounded by vertices (3,0),(8,0), and (36/7,20/7).
The final point is determined by equating
y=8-x
and
y=%284x-12%29%2F3
as shown here,
8-x=%284x-12%29%2F3
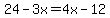
24-3x=4x-12
-7x=-36
x=36%2F7
Then
y=8-x
y=8-36%2F7
y=56%2F7-36%2F7
y=20%2F7
.
.
.
The max and min of F occur at the vertices of the feasible region.
Check all the points to determine.
.
.
.
(3,0)
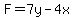
F=7y-4x
F=7%280%29-4%283%29
F=-12
.
.
.
(8,0)
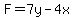
F=7y-4x
F=7%280%29-4%288%29
F=-32
.
.
.
(36/7,20/7)
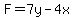
F=7y-4x
F=7%2820%2F7%29-4%2836%2F7%29
F=140%2F7-144%2F7
F=-4%2F7
.
.
.
The min value occurs at (8,0) where F=-32.