In the Gauss-Jordan elimination, you start with a system
of three equations and three unknowns:
 Then you convert it to this matrix:
Then you convert it to this matrix:
 Then you use row operations and end up with a matrix like this:
Then you use row operations and end up with a matrix like this:
 That is, you get 0's in the lower left three elements.
Then you convert back to a system of equations:
That is, you get 0's in the lower left three elements.
Then you convert back to a system of equations:
 Then you do what is called "back-substitution":
1. Solve the bottom equation for z.
2. Substitute that value of z in the middle equation,
and solve for y.
3. Substitute the values of y and z in the top equation
and solve for x.
----------
Then you do what is called "back-substitution":
1. Solve the bottom equation for z.
2. Substitute that value of z in the middle equation,
and solve for y.
3. Substitute the values of y and z in the top equation
and solve for x.
----------
 To get a 0 where the 3 is on the middle row:
Multiply the top row by -3 and the middle row by 7, and
add them together:
To get a 0 where the 3 is on the middle row:
Multiply the top row by -3 and the middle row by 7, and
add them together:
 --------------
--------------
 Replace the second row by that, leaving the rest as is
Replace the second row by that, leaving the rest as is
 To get a 0 where the 5 is on the bottom row:
Multiply the top row by -5 and the bottom row by 7, and
add them together:
To get a 0 where the 5 is on the bottom row:
Multiply the top row by -5 and the bottom row by 7, and
add them together:
 --------------
--------------
 Notice that as it turns out, we can divide that through
by -2, so we might as well do that too, and get:
Notice that as it turns out, we can divide that through
by -2, so we might as well do that too, and get:
 We replace the bottom row by that, leaving the rest as is
We replace the bottom row by that, leaving the rest as is
 To get a 0 where the 2 is on the bottom row:
Take the middle row as it is. Multiply the bottom row by 25, and
add them together:
To get a 0 where the 2 is on the bottom row:
Take the middle row as it is. Multiply the bottom row by 25, and
add them together:
 --------------
--------------
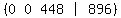 Notice that as it turns out, we can divide that through
by 448, so we might as well do that too, and get:
Notice that as it turns out, we can divide that through
by 448, so we might as well do that too, and get:
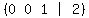 We replace the bottom row by that, leaving the rest as is
We replace the bottom row by that, leaving the rest as is
 Then we convert that back to this system of equations:
Then we convert that back to this system of equations:
 or rather,
or rather,
 Now we do what is called "back-substitution":
The bottom equation is already solved for z.
Substitute
Now we do what is called "back-substitution":
The bottom equation is already solved for z.
Substitute  in the middle equation:
in the middle equation:




 Substitute
Substitute  and
and  in the top
equation:
in the top
equation:





 So the solution is
So the solution is  Edwin
Edwin