SOLUTION: 1. Oil is dripping from a pipe at a constant rate and forms a circular pool. The area of the pool is increasing at 15cm^2/s. Find, to 3 significant figures, the rate of increase of

Algebra ->  Test -> SOLUTION: 1. Oil is dripping from a pipe at a constant rate and forms a circular pool. The area of the pool is increasing at 15cm^2/s. Find, to 3 significant figures, the rate of increase of      Log On


   

Question 163286: 1. Oil is dripping from a pipe at a constant rate and forms a circular pool. The area of the pool is increasing at 15cm^2/s. Find, to 3 significant figures, the rate of increase of the radius of the pool when the area is 50cm^2.
2. The region enclosed by the curve with equation y^2=16x, the x-axis and the lines x=2 and x=4 is rotated through 360º about the x-axis. Find, in terms of π, the volume of the solid generated.
3. A particle P moves in a straight line. At time t seconds, the displacement, s metres, of P from a fixed point O of the line is given by s=2tcost+t^2. Find, in m/s to 3 significant figures, the velocity of P when t=3.
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

1. Oil is dripping from a pipe at a constant rate and forms a circular pool. The area of the pool is increasing at 15cm^2/s. Find, to 3 significant figures, the rate of increase of the radius of the pool when the area is 50cm^2.

A+=+pi%2Ar%5E2

%28dA%29%2F%28dt%29=2%2Api%2Ar%28%28dr%29%2F%28dt%29%29

>>...The area of the pool is increasing at 15cm^2/s...<<

That says %28dA%29%2F%28dt%29=15.

So we substitute that and we have:

15=2%2Api%2Ar%28%28dr%29%2F%28dt%29%29

But we also have to substitute r when A=50

So we have to calculate r from A=pi%2Ar%5E2
when A=50 to find out what r is then.

A=pi%2Ar%5E2
50=pi%2Ar%5E2
50%2F%28pi%29=r%5E2
sqrt%2850%2F%28pi%29%29=r

So we substitute that in:

15=2%2Api%2Ar%28%28dr%29%2F%28dt%29%29

15=2%2Api%2Asqrt%2850%2F%28pi%29%29%28%28dr%29%2F%28dt%29%29

15=25.06628275%28%28dr%29%2F%28dt%29%29

15%2F25.06628275=%28dr%29%2F%28dt%29

.5984134206=%28dr%29%2F%28dt%29

Answer: .598cm%2Fsec

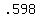
2. The region enclosed by the curve with equation y%5E2=16x, the x-axis and the lines x=2 and x=4 is rotated through 360º about the x-axis. Find, in terms of π, the volume of the solid generated. 

First we draw the graph of the parabola y%5E2=16x.

Taking square roots, we see this is really two graphs 
y=4sqrt%28x%29 and y=-4sqrt%28x%29


 
Next we'll draw in the vertical lines x=2 and x=4:



Now we'll erase everything that is not involved
in the rotation about the x-axis. That leaves only the 
graph of y=4sqrt%28x%29 between x=2 and x=4
and the x-axis.



We draw a slender rectangle as an element of area

.

Label the top point of the element (x,y),
and the height of it y: 



The formula for the volume of a vertically rotated function
using the disk method is:

V=+pi%2Aint%28%28RADIUS%29%5E2%2C+dx%2C+LEFTMOST_VALUE_OF_x%2C+RIGHTMOST_VALUE_OF_x+%29++

The height of that tiny rectangle is y and its width
is dx.

It is the height of that rectangle that will rotate 
about the x-axis, so the radius of rotation is y. The 
leftmost value of x is 2 and the rightmost value of x 
is 4.

V=+pi%2Aint%28%28y%29%5E2%2C+dx%2C+2%2C+4+%29++

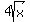
Then we replace y by 4sqrt%28x%29

V=+pi%2Aint%28%284sqrt%28x%29%29%5E2%2C+dx%2C+2%2C+4+%29++

V=+pi%2Aint%2816x%2C+dx%2C+2%2C+4+%29++
V=+16pi%2Aint%28x%2C+dx%2C+2%2C+4+%29++
V=+16pi%2A%28x%5E2%2F2%29matrix%283%2C2%2C%22%7C%22%2C4%2C%22%7C%22%2C%22+%22%2C%22%7C%22%2C2%29
V=+%288pi%29x%5E2matrix%283%2C2%2C%22%7C%22%2C4%2C%22%7C%22%2C%22+%22%2C%22%7C%22%2C2%29
V=+%288pi%29%284%5E2-2%5E2%29
V=+%288pi%29%2816-4%29
V=+%288pi%29%2812%29
V=+96pi

3. A particle P moves in a straight line. At time t seconds, the displacement, s metres, of P from a fixed point O of the line is given by s=2t%2Acost%2Bt%5E2. Find, in m/s to 3 significant figures, the velocity of P when t=3.

The velocity of P is the derivative of the displacement s with
respect to time t, that is, %28ds%29%2F%28dt%29.

s=2t%2Acos%28t%29%2Bt%5E2
%28ds%29%2F%28dt%29=2t%2A%28-sin%28t%29%29%2B+2cos%28t%29%2B2t++
%28ds%29%2F%28dt%29=-2t%2Asin%28t%29%2B2cos%28t%29%2B2t++
%28ds%29%2F%28dt%29=-2%28t%2Asin%28t%29-cos%28t%29-t+%29+

When t=3

%28ds%29%2F%28dt%29=-2%283%2Asin%283%29-cos%283%29-3%29

When calculating that be sure your calculator 
is in radian mode, not degree mode.

%28ds%29%2F%28dt%29=-0.317m%2Fs

Explanation of the negative sign:

Suppose the line on which P is moving is horizontal.
If a positive velocity means that P is moving to the
right, then a negative velocity means that P is moving
to the left.  So this negative velocity only indicates
that at the exact instant when 3 seconds have passed,
P is moving left.   

Edwin