Solve the simultaneous equations:
 Multiply the second equation through by 5 to
make the
Multiply the second equation through by 5 to
make the  -terms cancel when we add
the equations vertically term by term:
-terms cancel when we add
the equations vertically term by term:
 Adding them term by term:
Adding them term by term:
 Divide both sides by 67
Divide both sides by 67


 Factor:
Factor:

 Substitute
Substitute  into
into




 Divide both sides by
Divide both sides by  :
:



 So we have these solutions for
So we have these solutions for  ,
(x,y) = (6,8)
(x,y) = (6,-8)
Substitute
,
(x,y) = (6,8)
(x,y) = (6,-8)
Substitute  into
into




 Divide both sides by
Divide both sides by  :
:



 So we have these solutions for
So we have these solutions for  ,
(x,y) = (-6,8)
(x,y) = (-6,-8)
So there are four solutions:
(x,y) = (6,8)
(x,y) = (6,-8)
(x,y) = (-6,8)
(x,y) = (-6,-8)
-----------------------
What is the substitution for the quadratic formula for equation:
,
(x,y) = (-6,8)
(x,y) = (-6,-8)
So there are four solutions:
(x,y) = (6,8)
(x,y) = (6,-8)
(x,y) = (-6,8)
(x,y) = (-6,-8)
-----------------------
What is the substitution for the quadratic formula for equation:

 Since this already contains a small letter "a", we'll
write the quadratic formula using all CAPITAL LETTERS:
Since this already contains a small letter "a", we'll
write the quadratic formula using all CAPITAL LETTERS:
 where
where  ,
,  , and
, and 





 Using the +,
Using the +,
 Using the +,
Using the +,
 ------------------------------
What would the problem like at the beginning:
------------------------------
What would the problem like at the beginning:
 To clear of fractions, multiply second equation through
by 2:
To clear of fractions, multiply second equation through
by 2:
 Solve the second equation for y:
Solve the second equation for y:

 Substitute that in the first equation:
Substitute that in the first equation:







 Substitute each of those into:
Substitute each of those into:

 So there are 4 solutions:
(x,y)=(7,4)
(x,y)=(-7,-4)
(x,y)=(4,7)
(x,y)=(-4,-7)
----------------------
if the discriminant of a complete quadratic equation is 8,
what is the nature of its roots.
When the discriminant is positive, there are two different real solutions.
When it is 0 there is exactly one real solution
When it is negative there are no real solutions.
8 is positive so there are two different real solutions.
-----------------------
separate 72 into two parts so that the first part is the square of the second. let x represent the first part, what is the equation that would solve the problem.
The other part of
So there are 4 solutions:
(x,y)=(7,4)
(x,y)=(-7,-4)
(x,y)=(4,7)
(x,y)=(-4,-7)
----------------------
if the discriminant of a complete quadratic equation is 8,
what is the nature of its roots.
When the discriminant is positive, there are two different real solutions.
When it is 0 there is exactly one real solution
When it is negative there are no real solutions.
8 is positive so there are two different real solutions.
-----------------------
separate 72 into two parts so that the first part is the square of the second. let x represent the first part, what is the equation that would solve the problem.
The other part of  is
is 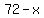 First part:
First part:  Second part:
Second part: 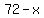 >>...the first part is the square of the second part...<<
So
>>...the first part is the square of the second part...<<
So







 So if x = first part = 81, then second part = 72-81=-9
That's kind of weird, separating 72 into 81 and -9, but
they do sum to 72, and certainly 81 is the square of -9.
Now if x = first part = 64, then second part = 72-64=8
That's not weird, separating 72 into 64 and 8, and
they do sum to 72, and certainly 64 is the square of 8.
So there are two answers, a weird one and one not weird at all.
Edwin
So if x = first part = 81, then second part = 72-81=-9
That's kind of weird, separating 72 into 81 and -9, but
they do sum to 72, and certainly 81 is the square of -9.
Now if x = first part = 64, then second part = 72-64=8
That's not weird, separating 72 into 64 and 8, and
they do sum to 72, and certainly 64 is the square of 8.
So there are two answers, a weird one and one not weird at all.
Edwin