Question 161909This question is from textbook college algebra
: can somebody help me solve this problem. i need to find the equation of the line with these characteristics. I need to express my answer using either the general form or the slope-intercept form of the equation of the line.
x-intercept=2; containing the point (4,-5)
i forgot how to find the slope with only the, x-intercept = 2 given.
This question is from textbook college algebra
Found 2 solutions by scott8148, Electrified_Levi:
Answer by scott8148(6628)   (Show Source):
Answer by Electrified_Levi(103)  (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
can somebody help me solve this problem. i need to find the equation of the line with these characteristics. I need to express my answer using either the general form or the slope-intercept form of the equation of the line.
x-intercept=2; containing the point (4,-5)
i forgot how to find the slope with only the, x-intercept = 2 given.
.
The slope intercept form of the equation is  , where "m" is the slope, "b" is the y-intercept
.
The x-intercept is the point where the line crosses the "x" axis
.
x intercept is given as the point ( p, 0 ) where "p" is the "x intercept number", in our case, it would be ( 2,0 )
.
Now we have another point (2,0)
.
Now that we have two points we can find the slope of the line
.
The two points are (2,0) and (4, -5)
.
(2,0)(x1,y1) and (4, -5)(x2,y2)
.
The slope equation is 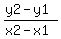 , we can replace the variables with numbers
.
Our slope = =  =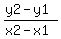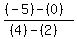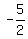 
.
Our slope =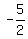
.
Our slope intercept form is , "m" is our slope, so we can replace "m" with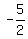
.
Our equation is now  , to find "b", we will replace "x" and "y" with one of our two points ( doesn't matter which one ) ( we will use point (2,0), replace "x" with "2", "y" with "0")
.
(2,0)(x,y) , =  =  , we will move (-5) to the left side
.
=  =  =  , we found "b", we can replace "b" with "5" in the original equation
.
=  = 
.
is the slope intercept form of the equation, for the general equation, we will multiply each side by "2"
.
=  =  =  =  , we will move (-5x) to the left side
.
=  =  , rearranging it becomes
.
= 
.
is the general/standard form, we can check our equation by replacing "x" and "y" with both of our two points
.
The two points are (2,0) and (4, -5)
.
(2,0)(x,y) = =  =  =  ( True )
.
(4, -5)(x,y) = =  =  =  = ( True )
.
is the slope-intercept form of the equation
.
is the general/standard form of the equation
.
This is the line on a graph
.
.
Hope I helped, Levi
|
|
|
