SOLUTION: FACTOR BY GROUPING {{{3AX+3AY+4X+4Y}}} FACTOR BY FINDING THE GREATEST COMMON FACTOR {{{25Y^5-15y^4+ 6y^3+5y^2}}}

FACTOR BY GROUPING



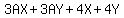In the first two terms only, 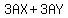, we can factor out
 and get .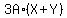


In the last two terms only, 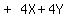, we can factor out
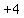 and get 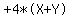.  So we have this:



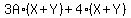Now we can take out the parentheses as the common factor
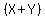 leaving the  and the ,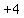
so the final factored form is:

 

--------------------------

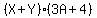FACTOR BY FINDING THE GREATEST COMMON FACTOR: 


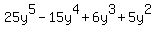We can factor  out of all the terms:



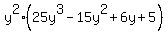That's as far as we can go, because there is no way
to factor what is inside the parentheses by grouping:

Edwin