Question 161686: log(2)8, log(4)8, log(8)8, log(16)8, log(32)8, log(64)8, log(128)8
find an expression of the nth term of the sequence. write expression in p/q form. justify using technology.
Answer by Earlsdon(6294)   (Show Source):
You can put this solution on YOUR website! Find the nth term ( ):
 , , , , , , ,...
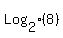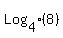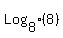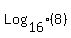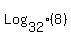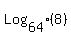You can see that the base of the logarithms is always 2 to some power, and the power of 2 goes up like this, starting with the first term  : , , , , , , ,..., so for the nth term the base would be:
Now you can write the nth term as:
 Now if you rewrite this in exponential form, you'll get:
 Substitute  to get:
 Now since the bases (2) are equal, the exponents must be equal, so...
 Divide both sides by n to get:
 This is the expression for the nth term expressed in  form.
|
|
|
