Question 16164: Hi there. I have a system, and I have tried to solve it two ways: substitution and table of values for each equation. Notice the lines should be perpendicular. When I graph them the lines are NOT perpendicular. When I solve by substitution, the answer I keep getting is (-3.2, -3.4) as a solution--which doesn't match the graph from the table of values. Help! Can you solve by substitution for me?
y=-1/2x-5
y=2x+3
Here's the table of values I got--the lines are NOT perpendicular but i can't figure out where I went wrong :(
For y=2x+3 my values were:
(-5, -7)
(-4, -5)
(-3, -3)
(-2, -1)
(-1, 1)
(0, 3)
(1, 5)
(2, 7)
(3, 9)
(4, 11)
(5, 13)
For y -1/2x=5, my values were:
(-5,-2.5 )
(-4, -3)
(-3, -3.5)
(-2, -4)
(-1, -4.5)
(0, -5)
(1, -5.5)
(2, -6.0)
(3, -6.5)
(4, -7)
(5, -7.5)
THANK YOU!!!!
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! You don't need a table of values to solve a system like this by substitution method.
Because y = y,
-1/2x-5=2x+3
Multiply both sides by the denominator which is 2:
-x - 10 = 4x + 6
Add +x to each side:
-x + x - 10 = 4x + x + 6
-10 = 5x + 6
Subtract 6 from each side:
-10 - 6 = 5x + 6 - 6
-16 = 5x
Divide both sides by 5, so  which is what you got.
It doesn't have to match the table of values, because the table of values usually ONLY includes whole number points. The table of values can't possibly include ALL the points because there are infinitely many of them.
So, you did it right! The table of values is NEVER complete, so unless you just happen to put y= -3.2 in each table.
The lines ARE perpendicular. If two lines are perpendicular, then the slope of one of the lines must be the NEGATIVE RECIPROCAL of the other line.
Here is the graph of these two lines:
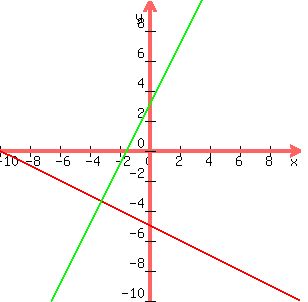
R^2 at SCC
|
|
|
