|
Question 161526: given the algebraic relation x=y^2+1, determine the domain, range, and whether or not it is a funtion. on my graphing calculator it shows a line that starts at (-.851,.386)to infinity. it shows it as though if you did a vertical line test, it would be a function. I'm confused because if I insert a pos # into y or a - # into y, squaring it will give you the same number. you can't have 2 different y's giving the same x or it is not a function, right?
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website! given the algebraic relation x=y^2+1, determine the domain, range, and whether or not it is a funtion.
I think you are a little confused. Before you enter it in
your calculator you must solve the equation for y:
 =±
This means the equation consists of two function graphs,
One function graph is the graph of this function, using
the positive square root:
=
The other function graph is the graph of this function,
using the negative square root:
But the original equation
consiste of BOTH of these at the same time on the
same set of axes, like this:
and this is not a function because it does not
pass the vertical line test. It is a parabola
that opens to the right.
Since the x-values of the graph start where x=1,
including that point, and the graph goes to
infinity on the right the domain is 
Since the y-values go both upward and downward
from 0 both to positive and negative infinity,
the range is 
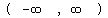No, it is not a function.
Edwin
|
|
|
| |
