|
Question 161503: The sum of two numbers is 15. Three times one of the numbers is 11 less than 5 imes the other. The answer is 7 and 8. I just don't know how to set it up to solve.
Found 3 solutions by Alan3354, gonzo, Electrified_Levi:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! The sum of two numbers is 15. Three times one of the numbers is 11 less than 5 imes the other. The answer is 7 and 8. I just don't know how to set it up to solve.
---------------
f = first number
s = second number
f+s = 15
3f + 11 = 5s
Use substitution
f = 15-s
------------
3*(15-s) + 11 = 5s
45-3s + 11 = 5s
56 = 8s
s = 7
f = 8
Answer by gonzo(654)  (Show Source):
You can put this solution on YOUR website! x = 1 of the numbers
y = the other number
-----
sum of the numbers equals 15 in equation form becomes
x + y = 15
three times one of the numbers equals 11 less than 5 times the other number in equation form becomes
3*x = 5*y - 11
-----
two equations to be solved simultaneously are:
x + y = 15
3*x = 5*y - 11
-----
in the second equation, subtract 5*y from both sides to get
3*x - 5*y = -11
equations are now both in the same form of a*x + b*y = c reproduced below.
x + y = 15
3*x - 5*y = -11
-----
multiply both sides of the first eqution by 3 to get
3*x + 3*y = 45
3*x - 5*y = -11
subtract the second equation from the first equation to get
0*x + 8*y = 56
effectively removing x from the equation to allow you to solve for y.
this becomes
8*y = 56
which becomes
y = 7
-----
original first equation is
x + y = 15
substituting 7 for y, we get
x + 7 = 15
subtracting 7 from both sides of the equation, we get
x = 15 - 7
which becomes
x = 8
-----
second original equation is
3*x = 5*y - 11
substituting 7 for y and 8 for x, we get
3*8 = 5*7 - 11
24 = 35 - 11
24 = 24
proving the values for x and y are correct.
-----
answers are:
x = 8
y = 7
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
The sum of two numbers is 15. Three times one of the numbers is 11 less than 5 imes the other. The answer is 7 and 8. I just don't know how to set it up to solve.
.
We have to name the two numbers, we will name the first number "x", the second "y"
.
There are two equations
.
(1) The sum of two numbers is 15. Since we know the numbers ("x" and "y"), we can put the words as an equation
.
The sum of two numbers( "x" and "y") is 15. =  =  , this is the first equation
.
(2) Three times one of the numbers is 11 less than 5 times the other. We know the numbers ( "x" and "y" ), we can put the words as an equation
.
Three times one of the numbers("x") is 11 less than 5 times the other("y") =  =  , this is the second equation
.
Our two equations are
.
(1)
.
(2)
.
These are systems of equations, we can solve these problems several ways.
.
This is the way I usually solve these problems
.
First solve for a letter in both equations (doesn't matter which one, usually the easiest), we will solve for "x" in both equations
.
(1) , to solve "x" we will move "y" to the right side
.
=  =  , rearranging, = 
.
, our first answer is 
.
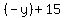
Lets solve "x" in our second equation
.
(2) , to solve "x" we will divide each side by "3"
.
=  = 
.
, our second answer is 
.
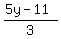
Our two answers are
.
.
.
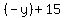
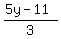
Since both our answers equal "x", the two answers equal each other
.
We can put them in an equation
.
 , now we just solve for "y"
.
= 
.
We will cross multiply
.
 =  =  , rearranging
.
=  , we will use distributive property
.
=  =  =  (since it was a negative "11")
.
, we will move (-3y) to the right side
.
=  =  , we will now move (-11) to the left side
.
=  ,  , divide each side by "8",
.
=  =  , rearranging, 
.
, "y" =  , we can find "x" by replacing "y" with "7" in one of our two equations
.
(1)
.
(2)
.
We will use the first equation (replace "y" with "7")
.
=  =  =  = 
.
, , you can check by replacing "x" with "8", "y" with "7", in both of our equations
.
(1) =  =  (True)
.
(2) =  =  =  ( True )
.
,
.
Hope I helped, Levi
|
|
|
| |
