Question 161042: CAN SOMEONE PLEASE HELP ME WITH THIS PROBLEM:
Use the discriminant to determine the number of real solutions of the equation.
2y^2 = -6y - 8
1, 2 or no real solutions
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
CAN SOMEONE PLEASE HELP ME WITH THIS PROBLEM:
Use the discriminant to determine the number of real solutions of the equation.

.
First we have to put the equation in stardard form  ( in this case, we have "y" instead of "x" ) ( in this case, we have "y" instead of "x" )
.
We need to move  to the right side, we will subtract to the right side, we will subtract  from each side from each side
.
 = =  = = 
.
If we rearrange,  = =  , or , or 
.
We will multiply each side by (-1), to make the variables positive
.
 = = 
.
 , we can divide each side by "2" to reduce the equation , we can divide each side by "2" to reduce the equation
.
 = =  = = 
.
 is the standard equation, is the standard equation,  , in our equation, a = 1, b = 3, c = 4 , in our equation, a = 1, b = 3, c = 4
.
The quadratic equation is 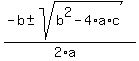 , the number in the radical , the number in the radical 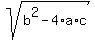 , will determine if the equation has one, two, or no real solutions, , will determine if the equation has one, two, or no real solutions,
.
( 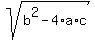 is considered the discriminant ) is considered the discriminant )
.
If the number inside the radical is positive, the equation will have two real solutions, if the number inside the radical is 0, the equation will have one solution, if the number inside the radical is negative, there are no real solutions to the equation, since you can't take the square root of a negative number.
.
In our equation  , a = 1, b = 3, c = 4 , a = 1, b = 3, c = 4
.
Lets replace the letters with our numbers in the quadratic equation
.
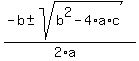 = = 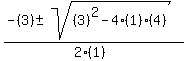 = =  = = 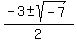
.
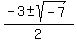 would be our answer, since the number inside the radical is negative ( would be our answer, since the number inside the radical is negative (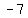 ) , this means the equation has no real solutions ) , this means the equation has no real solutions
.
Hope I helped, Levi
|
|
|