|
Question 160705This question is from textbook
: In a certain triangle the measure of one angle is double the measure of a second angle but is 5 degrees less than the measure of the third angle. If the sum of the measures of the three interior angles of a triangle is always 180 degrees, form an algebraic equation to express the problem, and identify the variables, coefficients, and constants of the alegbraic expression.
This question is from textbook
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a certain triangle the measure of one angle is double the measure of a second angle but is 5 degrees less than the measure of the third angle. If the sum of the measures of the three interior angles of a triangle is always 180 degrees, form an algebraic equation to express the problem, and identify the variables, coefficients, and constants of the algebraic expression.
:
Let the angles be A, B, C
:
Write an equation for each statement:
:
"the measure of one angle is double the measure of a second angle"
A = 2B
or
B = .5A
:
" but is 5 degrees less than the measure of the third angle."
A = C-5
or
C = (A+5)
:
"If the sum of the measures of the three interior angles of a triangle is always 180 degrees,":
A + B + C = 180
:
form an algebraic equation to express the problem, and identify the variables, coefficients, and constants of the algebraic expression.
:
Substitute for B and C
A + .5A + (A+5) = 180
2.5A = 180 - 5
2.5A = 175
solve
A = 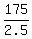
A = 70 degrees, B = 35, C = 75
|
|
|
| |