|
Question 160610: [ 8 10 -17]
[-5 -2 11]
[16 9 15]
[-4 20 4]
[-5 5 -15]
[-17 -7 -1]
I need to find the product of the two matrices. I know they look a little funny,im not sure how to get them set up right. The first one is a (3X3) and the second a (3x3), so i know it is defined, and the product is able to be found. I can do addiction,but im completly confused by multiplication. Id love to see the step and the correct answer. I really appericate your help!
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I need to find the product of the two matrices. I know they look a little funny,im not sure how to get them set up right. The first one is a (3X3) and the second a (3x3), so i know it is defined, and the product is able to be found. I can do addiction,but im completly confused by multiplication. Id love to see the step and the correct answer. I really appericate your help!
How do you multiply all of these numbers????

The first matrix has dimensions 3 down by 3 across.
That's a 3x3 matrix.
The second matrix has dimensions 3 down by 3 across.
That's a 3x3 matrix.
Write 3x3 3x3
The two (blue) inner dimensions are both 3. They must be the same
in order for the matrices to even be multipliable. If they weren't the
same, the multiplication would not be defined. Since they are both
3, they can be multiplied. The product matrix will have the two outer
(red) dimensions. They are both 3, so the product matrix will also be
a 3x3 matrix.
Set the product equal to a 3x3 matrix of blanks to
fill in.
 = =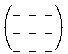 I won't go through all 9 blanks. I will only tell you how to fill in
three of them at random. Then you will know how to do the rest.
---
Let's fill in the blank which is in row 3 and column 2,
that's in the middle of the bottom row:
Take row 3 from the first matrix:
I won't go through all 9 blanks. I will only tell you how to fill in
three of them at random. Then you will know how to do the rest.
---
Let's fill in the blank which is in row 3 and column 2,
that's in the middle of the bottom row:
Take row 3 from the first matrix:
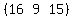 and column 2 of the second matrix:
and column 2 of the second matrix:
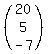 Multiply corresponding elements then add them all:
Multiply corresponding elements then add them all:
 = =
 So put a
So put a  in the blank in row 3 and column 2: in the blank in row 3 and column 2:
 = = ---
Next let's fill in the blank in the upper right hand corner.
That is the blank in row 1 and in column 3:
Take row 1 from the first matrix:
---
Next let's fill in the blank in the upper right hand corner.
That is the blank in row 1 and in column 3:
Take row 1 from the first matrix:
 and column 3 from the second matrix:
and column 3 from the second matrix:
 Multiply corresponding elements then add them all:
Multiply corresponding elements then add them all:
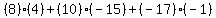 = =
 So put a
So put a 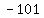 in the blank in row 1 and column 3,
that is, the upper right corner: in the blank in row 1 and column 3,
that is, the upper right corner:
 = = ----
One more!
Let's fill in the blank in row 2 and column 1:
Take row 2 from the first matrix:
----
One more!
Let's fill in the blank in row 2 and column 1:
Take row 2 from the first matrix:
 and column 1 of the second matrix:
and column 1 of the second matrix:
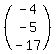 Multiply corresponding elements then add them all:
Multiply corresponding elements then add them all:
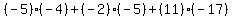 = =
 So put a
So put a 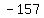 in the blank in row 2 and column 1: in the blank in row 2 and column 1:
 = = Do you see how to do it now? To fill in any blank in the
product matrix, you decide which row and column the blank
is in which you want to fill, then get the corresponding
row from the first matrix, and the corresponding column
from the second matrix, then multiply corresponding elements
and add them. You can fill them in in any order you choose.
When you fill in the rest of the blanks you should have this:
Do you see how to do it now? To fill in any blank in the
product matrix, you decide which row and column the blank
is in which you want to fill, then get the corresponding
row from the first matrix, and the corresponding column
from the second matrix, then multiply corresponding elements
and add them. You can fill them in in any order you choose.
When you fill in the rest of the blanks you should have this:
 = = Edwin
Edwin
|
|
|
| |