Question 160339: The area of a rectangle is 30 cm^2. The perimeter is 26cm. What are the length and width of the rectangle.
this is what i have so far
a=lw so 30= lw
p=2L + 2W so 26= 2L+2W
I'm not sure if I am supposed to substitute the first equation into the second one or just try to isolate L and w.
thanks.
Found 2 solutions by checkley77, Electrified_Levi:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! xy=30 or x=30/y
2x+2y=26
Now substitute (30/y) for x in the second equation & solve for y'
2(30/y)+2y=26
60/y+2y=26
(60+2y*y)/y=26
(60+2y^2)/y=26 now cross multiply;
60+2y^2=26y
2y^2-26y+60=0
2(y^2-13y+30)=0
2(y-10)(y-3)=0
y-10=0
y=10 answer.
y-3=0
y=3 answer.
Proof:
3*10=30
30=30
2*10+2*3=26
20+6=26
26=26
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
The area of a rectangle is 30 cm^2. The perimeter is 26cm. What are the length and width of the rectangle.
this is what i have so far
a=lw so 30= lw
p=2L + 2W so 26= 2L+2W
I'm not sure if I am supposed to substitute the first equation into the second one or just try to isolate L and w.
.
You did everything right so far.
.
You have the two equations
.

.

.
(You can reduce the second equation by dividing each side by "2",  = =  = =  = =  ) )
.
The two equations will =
.

.

.
We have two equations, or a system of equations
.
To find the "L" and "W", we will use the way I solve systems of equations, which is pretty easy
.

.

.
First solve for a letter ( doesn't matter which one, usually the easiest), we will solve for "W" in both equations
.
First equation 
.
To get "W" by itself we will divide each side by "L"
.
 = =  = =  , Our first answer = , Our first answer = 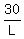
.
Second equation 
.
To get "W" by itself we will move "L" to the right side
.
 = =  = =  or or 
.
Our second answer = 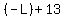
.
We can put our two answers in an equation, since both answers represent "W"(width), our two answers equal each other
.
 = = 
.
We will use cross multiplication
.
 = =  = = 
.
It becomes  = = 
.
This is a quadratic equation, we will put it in standard form(move "30" to the left side)
.
 = =  = = 
.
Standard form  Since this is a quadratic equation, we can use quadratic formula( We can solve by factoring, or completing the square as well, but I believe the formula is easiest) Since this is a quadratic equation, we can use quadratic formula( We can solve by factoring, or completing the square as well, but I believe the formula is easiest)
.
 , ,  , (a = (-1), b = 13, c = (-30) , (a = (-1), b = 13, c = (-30)
quadratic formula =  , replace the letters with numbers , replace the letters with numbers
.
 = =  = =  = =  = =
.
 = =  = = 
.
 = =  = = 
.
"L" can be either  or or 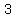
.
Just replace "L" in the second equation
.
 = =  = =  , or , or
.
 = =  = = 
.
Most likely  and and  , it could be the other way around, you can check by replacing these answers in the first two original equations. , it could be the other way around, you can check by replacing these answers in the first two original equations.
.
Hope I helped, Levi
|
|
|