 Notice that
Notice that  and that
and that  so
so  so replace
so replace 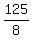 by
by 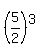 :
:
 Multiply exponents on the left:
Multiply exponents on the left:
 Distribute:
Distribute:
 Now observe that on the right the base
Now observe that on the right the base  is the
reciprocal of the base on the left, and the reciprocal
is the
is the
reciprocal of the base on the left, and the reciprocal
is the  power, so write
power, so write  on the right as
on the right as 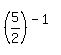 :
:
 Multiply the exponents on the right:
Multiply the exponents on the right:
 Distribute:
Distribute:
 Since both sides are powers of the same base, and
since that base is neither 0 nor 1, we may equate
the exponents and drop the bases:
Since both sides are powers of the same base, and
since that base is neither 0 nor 1, we may equate
the exponents and drop the bases:



 Edwin
Edwin