Question 160196: Find an equation of the circle with center at(-8,7) and passing through(1,-4) in the form of  where A,B,C are constant. Then where A,B,C are constant. Then
A=
B=
C=
Ive already have the answers for A B they are -8,7 I just how to find C if the radius is not provided
Found 2 solutions by Edwin McCravy, nerdybill:
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find an equation of the circle with center at(-8,7) and passing through (1,-4) in the form of  where A,B,C are constant. Then where A,B,C are constant. Then
A=
B=
C=
Ive already have the answers for A, B they are -8,7. I just
want to know how to find C if the radius is not provided.
So instead of:
 write
write

 Think now: What haven't you used that was given?
Answer: You haven't used this: "passing through (1,-4)"
So that means if you substitute (x,y) = (1,-4), the equation
must be true. So let's substitute that:
Think now: What haven't you used that was given?
Answer: You haven't used this: "passing through (1,-4)"
So that means if you substitute (x,y) = (1,-4), the equation
must be true. So let's substitute that:





 So write
So write 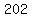 for for 
 and you're done. The radius is
and you're done. The radius is  .
Edwin .
Edwin
Answer by nerdybill(7384)   (Show Source): (Show Source):
|
|
|