Question 159787This question is from textbook Intermediate Algebra
: Please I have put this question up several times and no one has given me an answer.
A manufacturer produces two models of the same toy, Model A and Model B. Model A takes 4 hours to produce and costs $8 each. Model B takes 3 hours to produce and costs $7 each. If the manufacturer allots a total of 5800 hours and $12,600 for production each week, how many of each model will be produced?
Please show the steps. Thank you
This question is from textbook Intermediate Algebra
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A manufacturer produces two models of the same toy, Model A and Model B. Model A takes 4 hours to produce and costs $8 each. Model B takes 3 hours to produce and costs $7 each. If the manufacturer allots a total of 5800 hours and $12,600 for production each week, how many of each model will be produced?
:
Let A = no. of A model toys, Let B = no. of Model toys
:
Write an hours equation from the given information
4A + 3B = 5800
:
Write a cost equation also
8A + 7B = 12600
:
We can use elimination here,
Multiply the hours equation by 2, subtract from the cost equation:
:
8A + 7B = 12600
8A + 6B = 11600
------------------subtraction eliminates A, find B
0A + 1B = 1000
B = 1000 ea B models can be produced
:
Find A using the hrs equation:
4A + 3(1000) = 5800
4A + 3000 = 5800
4A = 5800 - 3000
4A = 2800
A = 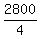
A = 700 A models can be produced.
;
:
Check solutions in the cost equation
8(700) + 7(1000) =
5600 + 7000 = 12600; confirms our solution
:
:
How about this? Were the steps understandable to you?
|
|
|