Question 159504: A tour-bus goes 90 miles to its destination. The rate returning is twice as fast as going. The time for a round trip is 3 hours. How fast does the tour-bus go on each part of the trip?
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Remember:  ---> --->  ... EQN 1 ... EQN 1
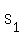 =Going destination =Going destination
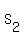 =Returning back= =Returning back= , twice as fast as going --> Condition 1 , twice as fast as going --> Condition 1
IMPORTANT:  , This distance is only for GOING for the trip. , This distance is only for GOING for the trip.
ALSO:  , Total time going + time returning = 3 hours, in this eqn we get -----> , Total time going + time returning = 3 hours, in this eqn we get -----> , EQN 2 , EQN 2
IMPORTANT: See EQN 1, time and Speed are inversely proportional. What does it mean? When Speed goes up, time goes down. Let's illustrate with this proportion:

You see, when you double 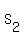 , then , then  doubles and vice versa, that's why INVERSELY PROPORTIONAL (not direct, not doubles and vice versa, that's why INVERSELY PROPORTIONAL (not direct, not 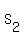 then then  ) )
Hope you got it because it's important when we apply it in getting 
.
With that said, as  , then , then  ,EQN 3, oks? ,EQN 3, oks?
Then we can equate EQN 2 and EQN 3 since both equal to  : :


 -----> -----> 

And, via EQN 2: 
Therefore we can continue in getting 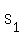 as per EQN 1: as per EQN 1:

 -----------------------> Speed going for the trip -----------------------> Speed going for the trip
And, as per Condition 1:
 ------------------> Speed returning back ------------------> Speed returning back
In doubt? go back EQN 1:




Thank you,
Jojo
|
|
|