Question 159345: Hi, Can someone please help me with these problems. I've tried to solve them and having a VERY HARD time. PLEASE, PLEASE!! Thank you,
1. You are planning to deposit $10,000 today into a bank account. Five years from today you expect to withdraw $7,500. If the account pays 5% interest per year, how much will remain in the account eight years from today?
2. What is the value (price) of a bond that pays $400 semiannually for 10 years and returns $10,000 at the end of 10 years? The market discount rate is 10% paid semiannually.
3. Combs, Inc. is issuing new common stock at a market price of $22. Dividends last year were $1.15 per share and are expected to grow at a rate of 7%. Flotation costs will be 5% of the market price. What is Combs, Inc.ís cost of external equity?
4. Frank Zanca is considering three different investments that his broker has offered to him. The different cash flows are as follows:
End of Year A B C
1 300 400
2 300
3 300
4 300 300 600
5 300
6 300
7 300
8 300 600
Because Frank has enough savings for only one investment, his broker has proposed the third alternative to be, according to his expertise, the best in town. However, Frank questions his broker and wants to eliminate the present value of each investment. Assuming a 15% discount rate, what is Frank's best alternative?
Answer by aka042(26)   (Show Source): (Show Source):
You can put this solution on YOUR website! For problem 1: You deposit $10,000 in a bank account today. Each year, you will earn 5% interest on whatever is in the bank account at the end of the year (or it will become 1.05 times bigger). For example, after 1 year, you will have (10,000)(1.05) = 10,500. After 2 years, you will earn not only 5% interest on your initial $10,000, but also on the $500 interest you earned in year one, because this is the current amount in your bank deposit. So we can right that the amount of money you have in your bank account in year two is (amt in year 1)*(1.05), or  which equals $11,025. which equals $11,025.
In general, the amount in your bank account at year n will be  . So after five years, you will have . So after five years, you will have  . Now, as the problem states, you withdraw $7500 from that amount, so . Now, as the problem states, you withdraw $7500 from that amount, so  . We want to find the balance at year 8, so that new balance must grow for another 3 years. Therefore, to find the balance at year 8, you will have . We want to find the balance at year 8, so that new balance must grow for another 3 years. Therefore, to find the balance at year 8, you will have  . We raise 1.05 to a power of 3 because 3 years elapse between year 5 and year 8. Therefore you have $6092.37 in your account after 8 years. . We raise 1.05 to a power of 3 because 3 years elapse between year 5 and year 8. Therefore you have $6092.37 in your account after 8 years.
For your second problem, you should look at the bond as an annuity... that is, a cash stream that pays an equal payment (the coupon payment) at a constant interval (in your case, every 6 months). The equation for the present value of an annuity (the price you are willing to pay today) is as follows: 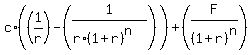 where c is the coupon in dollar terms, r is the discount rate, n is the number of periods, and F is the face value of the bond. Because this problem is in semiannual terms, we must multiply 10 by 2 to express years in semiannual periods (therefore you have 20 periods). I am not sure what is meant by the discount rate being 'paid semiannually', however if you are given the discount rate as an annual term, then you must divide it by 2 to get the term per period (5% per semiannum). However, if the discount rate is already given to you per 6 months, then you do not need to do this division. I am going to assume the latter, where the discount rate is quoted per 6 month period. Therefore, the price we are willing to pay for the bond today is as follows: where c is the coupon in dollar terms, r is the discount rate, n is the number of periods, and F is the face value of the bond. Because this problem is in semiannual terms, we must multiply 10 by 2 to express years in semiannual periods (therefore you have 20 periods). I am not sure what is meant by the discount rate being 'paid semiannually', however if you are given the discount rate as an annual term, then you must divide it by 2 to get the term per period (5% per semiannum). However, if the discount rate is already given to you per 6 months, then you do not need to do this division. I am going to assume the latter, where the discount rate is quoted per 6 month period. Therefore, the price we are willing to pay for the bond today is as follows: 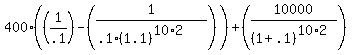 which comes out to be $4,891.86. This is the present value of the bond, or the price you are willing to pay for it today. which comes out to be $4,891.86. This is the present value of the bond, or the price you are willing to pay for it today.
For your third problem, we need to employ the Gordon Growth Model to find the Present value of the stock today (the cost to the company). The Gordon Growth Model states that  where PV is the present value of the share of the stock, D is the dividend paid today, r is the discount rate, g is your growth rate, and P is the price of the stock today. To find the dividend paid today, we must multiply last year's dividend by the growth rate to get: where PV is the present value of the share of the stock, D is the dividend paid today, r is the discount rate, g is your growth rate, and P is the price of the stock today. To find the dividend paid today, we must multiply last year's dividend by the growth rate to get:  . We can now find the PV of the dividend stream per share using the Gordon Growth Model: . We can now find the PV of the dividend stream per share using the Gordon Growth Model:  . Note you are not given r, the discount rate. r = your company's cost of external capital. We now need to determine floatation costs. These are simply .05 * $22 = $1.10 per share. Now note that for each share issued, the company earns $22. So we need to equate the cost of each share of stock to the company with the price the company is earning. Therefore, we have . Note you are not given r, the discount rate. r = your company's cost of external capital. We now need to determine floatation costs. These are simply .05 * $22 = $1.10 per share. Now note that for each share issued, the company earns $22. So we need to equate the cost of each share of stock to the company with the price the company is earning. Therefore, we have  which we can simplify to which we can simplify to  => =>  => =>  => =>  . Therefore, your company's cost of external capital is 12.89%. . Therefore, your company's cost of external capital is 12.89%.
For your final problem, we just need to find the discounted present value of each cash stream. Your first cash stream is an annuity receiving a 300 payment for 8 years. Therefore, given the annuity formula as described in problem 2, we have  = 1,346.20. For your second cash stream, we just have to discount each payment back its respective # of years. = 1,346.20. For your second cash stream, we just have to discount each payment back its respective # of years.  . Finally for the third cash stream, you just discount 600 back four years: . Finally for the third cash stream, you just discount 600 back four years:  . Cash stream A has the greatest PV therefore it is the best investment. . Cash stream A has the greatest PV therefore it is the best investment.
|
|
|