|
Question 159144: write an equation of the line containing the given point and perpendicular to the given line (8,-4); 6x+7y=2
Found 2 solutions by nerdybill, checkley77:
Answer by nerdybill(7384)   (Show Source):
You can put this solution on YOUR website! write an equation of the line containing the given point and perpendicular to the given line (8,-4); 6x+7y=2
.
First, let's rewrite the given formula into the "slope-intercept" form of a line:
y = mx + b
where
m is slope
b is the y-intercept
.
So, from:
6x+7y=2
7y=-6x+2
y = (-6/7)x + 2/7
.
Now, we know the slope is -6/7
If a line is to be perpendicular, the slope has to be the negative reciprocal:
M(-6/7) = -1
M = 7/6
This is the slope of a perpendicular line.
.
Plug our newly found slope, 7/6, and the given point (8,-4) into the "point-slope form" and solve:
y – y1 = m(x – x1)
y – (-4) = (7/6)(x – 8)
y + 4 = (7/6)x – (7/6)8
y + 4 = (7/6)x – (7/3)4
y + 4 = (7/6)x – (28/3)
y = (7/6)x – (28/3) - 4
y = (7/6)x – (28/3) - 12/3
y = (7/6)x – 40/3
Answer by checkley77(12844)  (Show Source):
You can put this solution on YOUR website! (8,-4); 6x+7y=2
7y=-6x+2
y=-6x/7+2/7 (red line) This line has a slope (m)=-6/7.
A perpendicular line has a slope=7/6.
Y=mX+B
-4=7/6*8+b
-4=56/6+b
b=-7-56/6
b=(-42-56)/6
b=-98/6
b=-49/3
y=7x/6-49/3 (green line).
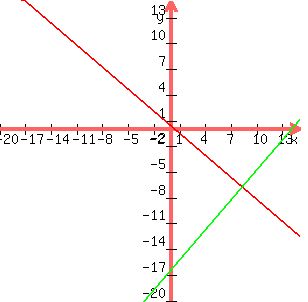 (graph 300x300 pixels, x from -20 to 15, y from -20 to 15, of TWO functions -6x/7 +2/7 and 7x/6 -49/3).
|
|
|
| |
