Question 159100: Determine the value of "a" so that the line through (5,8) and (a,6) has a slope of -3/4
Found 3 solutions by Fombitz, KnightOwlTutor, Electrified_Levi:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by KnightOwlTutor(293)   (Show Source): (Show Source):
You can put this solution on YOUR website! To determine the slope of the line M= y2-y1/x2-x1
(6-8)/(a-5)=-3/4
Cross multiply
4(-2)=-3a + 15
-8=-3a + 15
add 8 to both sides
0=-3a + 23
Add 3a to both sides
3a=23
divide both sides by 3
a=23/3
Plug in to check answer
I found the common denominator for the y values as 3
5X3=15
(6-8)/(23-15/3)=-2/8/3=-3/4
-2*inverse od 8/3 =-2*(3/8) simplfy the equation.
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Determine the value of "a" so that the line through (5,8) and (a,6) has a slope of 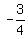
.
First we have to know what the slope is. The slope is how steep the line is. It is the slant of the line
.
These lines have negative slopes
.

.
As you can see, a slope that is negative means, the line (from left to right) is going down
.
Here are some lines with positive slopes
.

.
As you can see a slope that is positive, means the line(from left to right) is going up
.
Now that you know a little about slopes lets do the problem
.
Determine the value of "a" so that the line through (5,8) and (a,6) has a slope of 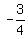
.
The slope is negative, so the line is going down(from left to right)
.
Here is one way to solve this kind of problem
.

.
If the point is (2,4) find a point (6,c) if the slope is 
.
The slope is negative, so the line is going down.
.
The slope is 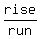 , or , or 
.
Since the slope is negative,  , ,
.
A slope of  means you go down "7" and over to the right "4" times means you go down "7" and over to the right "4" times
.
If we do that, we will get our point
.

.
The point is (6,-3)
.
There is yet another way to solve this kind of problem
.
Determine the value of "a" so that the line through (5,8) and (a,6) has a slope of 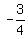
.
We use the slope equation = 
.
(ex. slope of (1,2)(x1,y1) and (2,4)(x2,y2), equation = 
.
Replace the variables
.
 = = 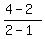 = = 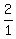 , these two lines have slope of "2" , these two lines have slope of "2"
.
we can do the same for our problem
.
Determine the value of "a" so that the line through (5,8)(x1,y1) and (a,6)(x2,y2) has a slope of 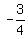
.
Replace the variables in the equation =  = = 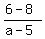 = = 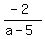 , we already know the slope, this equation we have = , we already know the slope, this equation we have = 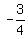
.
Our equation =  , now just solve for "a" , now just solve for "a"
.

.
We will use cross multiplication
.
 = =  = =  = = 
.
Using distribution
.
 = =  = =  = =  ( since the "5" is negative, it will make a positive "15" since the "3" is negative too) ( since the "5" is negative, it will make a positive "15" since the "3" is negative too)
.
We will move "15" to the left side
.
 = =  = = 
.
We will multiply each side by (-1)
.
 = =  = =  = =  , divide each side by "3" to get our "a" , divide each side by "3" to get our "a"
.
 = =  = = 
.
We can check by replacing "a" with 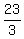 in our equation in our equation
.
 = =  = =  = =  = =  = =  = =  (True) (True)
.
a = 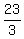
.
We found our point, if our point was (a,6), just replace "a" with 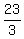 , our point is ( , our point is (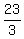 ,6) ,6)
.
Here are the two points

.
Now draw a line through these points, this line has a slope of 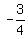
.

.
The line equation =  (slope -intercept form), or (slope -intercept form), or  (standard form) (standard form)
.
The point you were looking for is (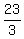 ,6) ,6)
.
Your answer is (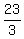 ,6) ,6)
.
Hope I helped, Levi
|
|
|