Question 159065: Suppose that the number of new homes built, H, in a city over a period of time, t, is graphed on a rectangular coordinate system where time is on the horizontal axis. Suppose that the number of homes built can be modeled by an exponential function, H= p * at , where p is the number of new homes built in the first year recorded. If you were a homebuilder looking for work, would you prefer that the value of a to be between 0 and 1 or larger than 1? Explain your reasoning.
Thank you for helping me out on this =]
Answer by gonzo(654)   (Show Source): (Show Source):
You can put this solution on YOUR website! the answer is if it's 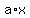 , any a value is ok but the bigger the x value the better. if it's , any a value is ok but the bigger the x value the better. if it's  , any value > 1 is good because there will be growth, and any value < 1 is not good because there will be no growth. , any value > 1 is good because there will be growth, and any value < 1 is not good because there will be no growth.
--------------------------------------------
to show you, i'll graph 5 equations with different (a) values used in each equation starting with a value of 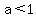 and ending with a value of and ending with a value of 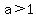 . .
---------------------------------------------
so that the graphs will show the proper x-axis values and the proper y-axis values, i had to cross the origin with both x and y values.
for your purposes, you just need to look at the values where x >= 0.
disregard the values where x < 0 since they are there only to force the x-axis and y-axis to show up properly and have no other meaning for the discussion.
-----------------------------------------
in both of these graphs, i am showing the total number of houses projected each year. any growth will be the number of houses in that year minus the number of houses in the previous year.
------------------------------------------
for linear growth, the general equation will be 
where
y is the total number of homes in each year (thousands).
x is the number of years.
a is the multiplication factor for each year.
h is the starting number of houses in thousands.
h will be set to 100 (thousand).
the additional h is required to make the number of houses equal to 100 (thousand) when x = 0.
-------------------------------------------
for the first equation, a is set to .25
for the second equation, a is set to .5
for the third equation, a is set to .75
for the 4th equation, a is set to 1.00
for the 5th equation, a is set to 1.25
---------------------------------------------
scan down below the graph for more information.
------------------------------------------------

----------------------------------------------
the growth of homes in each year is the number of houses in that year minus the number of houses in the previous year.
as a gets larger, the number of houses required in a year goes higher.
for example,
in year 10 with a = .25, the number of houses is 350.
in year 10 with a = .75, the number of houses is 850.
in year 10 with a = 1.25, the number of houses is 1350.
--------------------------------------------------------
for exponential growth, the general equation will be 
where
y is the total number of homes in each year.
x is the number of years.
a is the base factor that will be raised to the x power for each year.
h is the starting number of houses in thousands.
h will be set to 100 (thousand).
the additional h is not required here because a^0 = 1 for all values of a.
-------------------------------------------
for the first equation, a is set to .25
for the second equation, a is set to .5
for the third equation, a is set to .75
for the 4th equation, a is set to 1.00
for the 5th equation, a is set to 1.25
---------------------------------------------
scan down below the graph for more information.
------------------------------------------------

------------------------------------------------------
with an exponential factor, interesting things happen.
when a is > 1, the growth takes off.
when a = 1 there is no growth.
when a < 1 there is actually a decrease in the number of houses required each year.
if we take year 6 as an example, we get the following values:
when a = .25,  which equals .0244....., a number very close to 0. which equals .0244....., a number very close to 0.
when a = .50,  which equals 1.5625, a number still very close to 0. which equals 1.5625, a number still very close to 0.
when a = .75  which equals 17.7978..., a number that is further away from 0 but still less then the starting value of 100. which equals 17.7978..., a number that is further away from 0 but still less then the starting value of 100.
when a = 1.00  which equals 100. the number of houses required each year remains the same. which equals 100. the number of houses required each year remains the same.
when a = 1.25  which equals 381.469.... which equals 381.469....
-----------------------------------------
as x gets larger, any value of a less than 1 will tend towards 0.
take x = 100
.25^100 = 6.223.....^-61 which is a very small number and will keep getting smaller as x gets larger.
.75^100 = 3.207.....^-13 which is still avery small number and will keep getting smaller as x gets larger.
1.0^100 = 1 and will always be 1 as x gets larger because 1 to any power = 1.
1.25^100 = 4.909...^9 which is a very big number and will keep getting bigger as x gets large
|
|
|