Question 158976: The length of a rectangular playing field is 5 meters less than twice its width. if 230 meters of fencing goes around the field, find the dimensions of the field.
Found 2 solutions by checkley77, Electrified_Levi:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! L=2W-5
2W+2(W-5)=230
2W+2W-10=230
4W=230+10
4W=240
W=240/4
W=60 METERS FOR THE WIDTH.
L=2*60-5
L=120-5
L=115 METERS FOR THE LENGTH.
PROOF:
2*60+2(60-5)=230
120+2*55=230
120+110=230
230=230
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help
.
The length of a rectangular playing field is 5 meters less than twice its width. if 230 meters of fencing goes around the field, find the dimensions of the field.
.
First we have to find variables for length and width
.
The length of a rectangular playing field is 5 meters less than twice its width.
.
We can name the width "x"
.
The length of a rectangular playing field is 5 meters less than twice its width, if the width is "x", and the length is 5 meters less than twice the width, this is how you right the length, 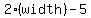 , width = "x" , width = "x" 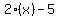 = = 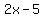
.
The length = 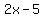
.
The width = 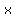
.
Since 230 meters of fencing goes around the field, we are trying to find the Perimeter of the field
.
The length = 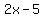
.
The width = 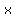
.
The Perimeter of a Rectangle is = 
.
They give us the Perimeter, 230 meters, so we can replace "Perimeter" with "230"
.
 = = 
.
Since the width = 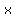 , and the length = , and the length = 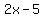 , we can replace "width" and "length" with our variables , we can replace "width" and "length" with our variables
.
 = =  , now just solve for "x" , now just solve for "x"
.
We will get rid of the parentheses, and use distribution
.
 = =  = =  = =  (Since the "5" is negative the number will be negative) (Since the "5" is negative the number will be negative)
.
Add like terms
.
 = =  = = 
.
We will move (-10) to the right side
.
 = =  = =  , To solve "x" we will divide each side by "6" , To solve "x" we will divide each side by "6"
.
 = =  = =  = = 
.
x = "40", we can check by replacing "x" with "40" in our equation
.
 = =  = =  = =  = =  = =  ( True ) ( True )
.
x = "40"
.
Our width and length in variable form were:(Just replace "x" with "40" in our equations)
.
The length = 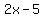 = = 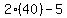 = = 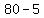 = 75 = 75
.
The width =  = 40 = 40
.
Since the unit is the meter, our answers would be
.
The Length = 75 meters
.
The Width = 40 meters
.
Hope I helped, Levi
|
|
|