Question 158862: 1. two cars enter a Florida Turnpike at 8:00am, each heading for Wildwood. one car average speed is 10 miles per hour more than the other. The faster car arrives at Wildwood at 11:00am, 1/2 hours before the other car. What is the average speed of each car? How far did each travel.
2. Am object is propelled upward with an initial velocity of 20 meters per second. The distance, in meter, of the object from the ground after t seconds is s=-4.9t+20t.
a. when will the object be 15 meters above the ground?
b. when will it strike the ground?
c. will the object reach a height of 100 meters?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. two cars enter a Florida Turnpike at 8:00am, each heading for Wildwood. one car average speed is 10 miles per hour more than the other. The faster car arrives at Wildwood at 11:00am, 1/2 hours before the other car. What is the average speed of each car? How far did each travel.
:
Fast car travel time = 3 hrs
Slow car travel time = 3.5 hrs
:
Let s = speed of the slower car
then
(x+10) = speed of the faster car
:
Both cars traveled the same distance, write a distance equation
Dist = time * speed
:
slow car dist = fast car dist
3.5s = 3(s+10)
3.5s = 3s + 30
3.5s - 3s = 30
.5s = 30
s = 60 mph is the slow car
and
60 + 10 = 70 mph is the speed of the fast car
:
Find the dist using the slow car expression
3.5 * 60 = 210 mi
Check solutions by finding the dist using the fast car expression
3 * 70 = 210 mi
:
:
2. Am object is propelled upward with an initial velocity of 20 meters per second. The distance, in meter, of the object from the ground after t seconds is s=-4.9t+20t. I think this should be -4.9t^2 + 20t
:
a. when will the object be 15 meters above the ground?
:
-4.9t^2 + 20t = 15
-4.9t^2 + 20t - 15 = 0
Use the quadratic formula, we get two positive solutions:
t ~ 1 sec (on the way up)
and
t ~ 3.1 (on the way down)
b. when will it strike the ground?
:
When it strikes the ground, s = 0
-4.9t^2 + 20t = 0
-t(4.9t - 20) = 0
4.9t - 20 = 0
4.9t = +20
t = 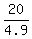
t = 4.1 sec
;
:
c. will the object reach a height of 100 meters?
;
Obviously it won't, max will occur around 2 sec
h = -4.9(2^2) + 20(2)
h = -19.6 + 40 = 20.4 ft, not even close
|
|
|