Question 158310: A farmer buys 100 animals for $100.00. The animals include at least one cow, one pig, and one chicken, but no other kind. If a cow costs $10.00, a pig costs $3.00, and a chicken costs $0.50, how many of each did he buy?
Answer by ptaylor(2198)   (Show Source):
You can put this solution on YOUR website! This problem has been around for a looooong time. It's yet another example of having more unknowns than equations. In problems such as this, it's usually necessary to apply a great deal of trial and error coupled with the constraints inherent in the problem. Many times, there is more than one solution.
Let x=number of chickens
y=number of pigs
z=number of cows
Now we are told that:
x+y+z=100----------------------------eq1
we are also told that:
0.5x+3y+10z=100------------------------eq2
Multiply eq 2 by 2 and then subtract eq1 from it and we get:
5y+19z=100
subtract 19z from each side
5y=100-19z divide each side by 5
y=(100-19z)/5----eq2a --- this equation gives us a relationship between the number of pigs (y) and the number of cows (z).
Now we know a couple of things that will help us to solve this problem:
(1) We cannot have fractions of animals ---we are dealing with whole numbers
(2) We cannot have negative animals----we are dealing with positive numbers
(3) We must, at least, have one of each animal
By inspecting eq2a, we can quickly see that we cannot have more than 5 cows otherwise we start getting negative pigs. So, lets do some trial and error:
If we have 5 cows-----------------y=(100-95)/5=1 BINGO!!
So, 5 cows and 1 pig are possibilities
Lets substitute these values into eq1 and see if they work for chickens:
x+1+5=100
x=94 chickens
Clearly the numbers check; let's see if the values check:
94*0.5+1*3.00+ 5*10=100
47+3+50=100
100=100
So, 94 chicks, 1 pig and 5 cows work
Let's see if we have other possibilities:
If we have 4 cows-----y=(100-76)/5----No!!! we get fractions of pigs
If we have 3 cows-----y=(100-57)/5----No!!! we get fractions of pigs
If we have 2 cows-----y=(100-38)/5----No!!! we get fractions of pigs
If we have 1 cow------y=(100-19)/5----No!!! we get fractions of pigs again
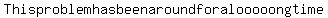 0 cows would also work if the problem allowed}}
Hope this helps---ptaylor
|
|
|
