
What is between the absolute value bars,
 , can either be negative or
non-negative, so we must always make two
separate equations, one for each case:
Case 1:
, can either be negative or
non-negative, so we must always make two
separate equations, one for each case:
Case 1:
 Then
Then  is non-negative and
we can just replace the absolute value bars
by parentheses, so
is non-negative and
we can just replace the absolute value bars
by parentheses, so
 becomes simply:
becomes simply:



 Case 2:
Case 2:
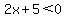 Then
Then  is negative and so we
must multiply what is between the absolute
value bars by -1 to make it a positive
number, so w replace
is negative and so we
must multiply what is between the absolute
value bars by -1 to make it a positive
number, so w replace 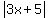 by
by
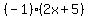 . So
. So
 becomes
becomes 



 But we must check both solutions because
sometimes we get extraneous solutions,
that is, bogus solutions, that do not check,
and these must be discarded.
Checking
But we must check both solutions because
sometimes we get extraneous solutions,
that is, bogus solutions, that do not check,
and these must be discarded.
Checking  in original:
in original:





 So
So  is a solution.
Checking
is a solution.
Checking  in original:
in original:





 So
So  is also a solution.
The solutions are -1 and -3.
Edwin
is also a solution.
The solutions are -1 and -3.
Edwin