|
Question 158073: Can someone help me with this one.
Determine whether the graphs of the equations are parallel lines, perpendicular lines or niether.
3x - 8y = -18
32x + 12y = -18
Thank you!
Found 3 solutions by jim_thompson5910, Earlsdon, Electrified_Levi:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
Answer by Earlsdon(6294)   (Show Source): (Show Source):
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Can someone help me with this one.
Determine whether the graphs of the equations are parallel lines, perpendicular lines or niether.


Thank you!
.
First we have to get the two lines in the slope intercept form, ("m" is the slope, "b" = y intercept) ("m" is the slope, "b" = y intercept)
.
First equation
.

.
We will move (-8y) to the right side
.
 = =  = = 
.
We will move (-18) to the left side
.
 = =  = = 
.
 = =  , To get it in slope intercept form, we have to divide each side by "8" , To get it in slope intercept form, we have to divide each side by "8"
.
 = =  = = 
.
 = =  = = 
.
 is the slope intercept equation of is the slope intercept equation of  , we can check our answer by replacing "x" and "y" with any point on the line, in both of the different forms of equation , we can check our answer by replacing "x" and "y" with any point on the line, in both of the different forms of equation
.
We will use the points (-6,0)(x,y) and ( 2, 3)(x,y)( replace "x" with (-6), replace "y" with "0" for our first check, replace "x" with "2", replace "y" with "3" in our second check
.
(-6,0),  = =  = =  = =  (True) (True)
.
(-6,0),  = =  = =  = =  = =  (True) (True)
.
Lets check with a different point
.
(2,3) ,  = =  = =  = =  (True) (True)
.
(2,3) ,  = =  = =  = =  = =  = =  (True) (True)
.
 is our first answer is our first answer
.
Second equation (We are changing equation into slope intercept form  ) )
.

.
We need to move "32x" to the right side
.
 = =  = = 
.
 = =  , To get the equation in slope intercept form, we will divide each side by "12" , To get the equation in slope intercept form, we will divide each side by "12"
.
 = =  = =  = = 
.
 = = 
.
The slope intercept form of the equation  is is 
.
Lets check using two points again, Lets use (0,  ) and ( ) and (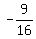 , 0)(We will do the first point first) , 0)(We will do the first point first)
.
(0,  ), ),  = =  = =  = =  (True) (True)
.
(0,  ), ),  = =  = =  = =  (True) (True)
.
Second check(second point)
.
(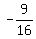 , 0) , , 0) ,  = =  = =  = =  (True) (True)
.
(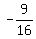 , 0), , 0),  = =  = =  = =  = =  (True) (True)
.
 is our second answer. is our second answer.
.
Our two equations in slope intercept form are
.

.

.
The slope of the first line is 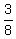 , the slope of the second line is , the slope of the second line is 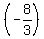
.
If two lines are parallel, their slopes would be the same(our lines are not parallel)
.
If two lines are perpendicular, their slopes are the negative reciprocal of each other
.
(examples of negative reciprocals: 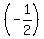 and and  , ,  and and 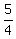 , , 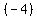 and and 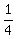 , to find the negative reciprocal of a number, switch the denominator and numerator with each other and add a negative sign) , to find the negative reciprocal of a number, switch the denominator and numerator with each other and add a negative sign)
.
Our two lines are perpendicular, 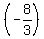 is the negative reciprocal of is the negative reciprocal of 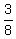 ( the numbers to the right of the "x" ( the numbers to the right of the "x"  , Our "b's" don't have to be the same) , Our "b's" don't have to be the same)
.
Here are the two lines in a graph( lines are in slope-intercept form)
.
 = green line = green line
.
 = red line = red line
.

.
As you can see the lines are perpendicular
.
Hope I helped, Levi
|
|
|
| |