|
Question 158031This question is from textbook
: Review Exercises Chapter 1
Find an equation of the line having the given characteristics. Write the equation using the general form or the slope-intercept form, whichever you prefer. Graph each line.
9. Slope = -3; containing the point (2, -1)
y = -3x - 1 this is where I started
This question is from textbook
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! First let's find the equation of the line
If you want to find the equation of line with a given a slope of  which goes through the point (2,-1), you can simply use the point-slope formula to find the equation: which goes through the point (2,-1), you can simply use the point-slope formula to find the equation:
---Point-Slope Formula---
 where where  is the slope, and is the slope, and ) is the given point is the given point
So lets use the Point-Slope Formula to find the equation of the line
 Plug in Plug in  , ,  , and , and  (these values are given) (these values are given)
 Rewrite Rewrite  as as 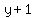
 Distribute Distribute 
 Multiply Multiply  and and  to get to get 
 Subtract 1 from both sides to isolate y Subtract 1 from both sides to isolate y
 Combine like terms Combine like terms  and and  to get to get 
------------------------------------------------------------------------------------------------------------
Answer:
So the equation of the line with a slope of  which goes through the point (2,-1) is: which goes through the point (2,-1) is:
 which is now in which is now in  form where the slope is form where the slope is  and the y-intercept is and the y-intercept is 
Since  this tells us that the y-intercept is this tells us that the y-intercept is ) .Remember the y-intercept is the point where the graph intersects with the y-axis .Remember the y-intercept is the point where the graph intersects with the y-axis
So we have one point )

Now since the slope is comprised of the "rise" over the "run" this means

Also, because the slope is  , this means: , this means:

which shows us that the rise is -3 and the run is 1. This means that to go from point to point, we can go down 3 and over 1
So starting at ) , go down 3 units , go down 3 units

and to the right 1 unit to get to the next point )

Now draw a line through these points to graph 
 So this is the graph of So this is the graph of  through the points through the points ) and and )
Also, notice how the graph has a slope of -3 (since  ) and it goes through the point (2,-1). ) and it goes through the point (2,-1).
|
|
|
| |