|
Question 157772: Find four consecutive integers such that twice the first subtracted from the sum of the other three integers is sixteen.
Found 3 solutions by checkley77, jojo14344, Electrified_Levi:
Answer by checkley77(12844)   (Show Source): (Show Source):
You can put this solution on YOUR website! Integers=x,x+1,x+2,x+3
(x+1+x+2+x+3)-2x=16
3x+6-2x=16
x=16-6
x=10 answer for the first integer.
10,11,12,13 are all the integers.
proof:
11+12+13-2*10=16
36-20=16
16=16
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let ¨x= 1st integer
x+1 = 2nd integer
x+2 = 3rd integer
x+3 = 4th integer
Then, (x+1+x+2+x+3)-2x=16 ----------------------- condition, twice the 1st is subtracted from the sum of 2nd, 3rd & 4th:
continuing;
3x-2x=16-6
x=10 ------------------------------------- 1st integer
10+1=11 ---------------------------------- 2nd integer
10+2=12 ---------------------------------- 3rd integer
10+3=13 ---------------------------------- 4th integer
To check, go back to the condition:
11+12+13-2(10)=16
36-20=16
16=16
Thank you,
Jojo
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi,Hope I can help
.
Find four consecutive integers such that twice the first subtracted from the sum of the other three integers is sixteen.
.
consecutive means " in order"(examples: 45,46,47,48 . Sunday, Monday, Tuesday)
.
To find the 4 consecutive numbers, we have to find the variables for all four numbers
.
Since consecutive means " in order "(we are trying to find 4 numbers that come right after the other(example of consecutive numbers: 22,23,24,25,26)
.
We can always name the first number of any "consecutive numbers" - "x"
.
"x" is our first number, to find the other numbers, we will add "1" each time(we are trying to find numbers that come right after the other)
.
2nd number = (add "1" to our first number "x") = "x+1"
3rd number = (add "1" to the second number "x + 1", ("x + 1 + 1")) = "x+2"
4th number = (add "1" to the third number "x+2",("x+2+1")) = "x+3"
.
(If there was a fifth number you would add "1" to the fourth number "x+3" = "x+4", the sixth number would be "1" added to the fifth number "x+4" = "x+5", you get the idea)(If you were solving for consecutive odd or even numbers, you would add "2" every time, consecutive even/odd number = ( x, x + 2, x + 4, x + 6, x + 8, ...)
(examples of consecutive even/odd number: 3, 5, 7, 9 : 16, 18, 20, 22))
.
Since we are solving for just consecutive numbers, our numbers are
.
1st number = " " "
2nd number = " " "
3rd number = " " "
4th number = " " "
.
Now we can replace these variables with the problem, and solve for the numbers
.
Find four consecutive integers such that twice the first subtracted from the sum of the other three integers is sixteen.
.
If we replace the variables in the problem, and put the word problem in an equation, the equation = 
.
Now we just solve for "x"
.

.
We will remove the first set of parentheses,we will multiply 2(x)
.
 = = 
.
We will remove the other sets of parentheses
.
 = = 
.
We will rearrange the equation, so we can add/subtract like terms
.
 = = 
.
We will add/subtract like terms
.
 =, (x+x+x-2x)(+1+2+3) = 16, = =, (x+x+x-2x)(+1+2+3) = 16, = 
.
To solve for "x" we will move "6" to the right side
.
 = =  = =  = = 
.
"x" = "10" , we can check by replacing "x" with our equation
.
 = = 
.
 = = 
.
 = = 
.
 = =  = =  = =  = =  (True) (True)
.
Here is our number variables again (To find the numbers, replace "x" with "10")
.
1st number = " ", " ", " " "
2nd number = " ", " ", " ", " ", "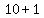 ", " ", " " "
3rd number = " ", " ", "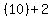 ", " ", "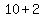 ", " ", " " "
4th number = " ", " ", "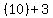 ", " ", "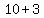 ", " ", " " "
.
Find four consecutive integers such that twice the first subtracted from the sum of the other three integers is sixteen. (  = =  = =  = =  (True)) (True))
.
1st number = 
2nd number = 
3rd number = 
4th number = 
.
Hope I helped, Levi
|
|
|
| |