SOLUTION: 7.08x^6 + 4.15x^3 - 9.6 = 0 Is it possible to factor this equation? I would really appreciate the help. Thanks

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: 7.08x^6 + 4.15x^3 - 9.6 = 0 Is it possible to factor this equation? I would really appreciate the help. Thanks      Log On


   

Question 157688: 7.08x^6 + 4.15x^3 - 9.6 = 0
Is it possible to factor this equation? I would really appreciate the help.
Thanks
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
7.08x^6 + 4.15x^3 - 9.6 = 0
Is it possible to factor this equation? I would really appreciate the help.
-----------------
Yes, it's possible but the coefficients are messy.
This is a quadratic in term of x^3, that is, it's
7.08(x^3)^2 + 4.15(x^3) - 9.6 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 7.08x%5E2%2B4.15x%2B-9.6+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284.15%29%5E2-4%2A7.08%2A-9.6=289.0945.

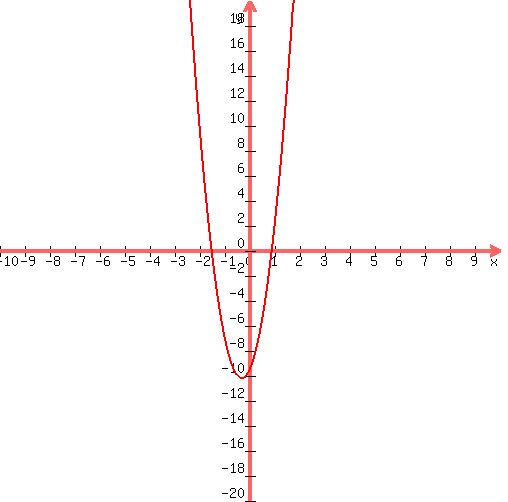
Discriminant d=289.0945 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-4.15%2B-sqrt%28+289.0945+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%284.15%29%2Bsqrt%28+289.0945+%29%29%2F2%5C7.08+=+0.90768214580453
x%5B2%5D+=+%28-%284.15%29-sqrt%28+289.0945+%29%29%2F2%5C7.08+=+-1.49384033789493

Quadratic expression 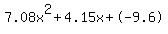7.08x%5E2%2B4.15x%2B-9.6 can be factored:
7.08x%5E2%2B4.15x%2B-9.6+=+%28x-0.90768214580453%29%2A%28x--1.49384033789493%29
Again, the answer is: 0.90768214580453, -1.49384033789493. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+7.08%2Ax%5E2%2B4.15%2Ax%2B-9.6+%29


The onsite solver always divides out the coefficient of the highest order term, but you can use the quadratic equation to find the roots, then use them to factor the polynomial.
The factors are not integers.